题目内容
7. 对某班40名高中学生是否喜欢数学课程进行问卷调查,将调查所得数据绘制成二维条形图如图所示.
对某班40名高中学生是否喜欢数学课程进行问卷调查,将调查所得数据绘制成二维条形图如图所示.(Ⅰ)根据图中相关数据完成以下2×2列联表,并计算有多大把握认为性别与是否喜欢数学有关系?
| 喜欢数学课程 | 不喜欢数学课程 | 总计 | |
| 男 | |||
| 女 | |||
| 总计 | 40 |
参考公式:K2=$\frac{(a+b+c+d)(ad-bc)^{2}}{(a+b)(c+d)(a+c)(b+d)}$.
临界值附表:
| P(K2≥k0) | 0.5 | 0.4 | 0.25 | 0.15 | 0.1 | 0.01 |
| k0 | 0.455 | 0.708 | 1.323 | 2.072 | 2.706 | 6.635 |
分析 (1)根据条形图所给数据,得2×2列联表;根据列联表所给的数据,代入求观测值的公式,求出观测值,即可得出结论.
(2)确定基本事件的个数,利用公式求出女生A被选中的概率.
解答 解:(1)根据条形图所给数据,得2×2列联表为
| 喜欢数学课程 | 不喜欢数学课程 | 总计 | |
| 男 | 15 | 10 | 25 |
| 女 | 5 | 10 | 15 |
| 总计 | 20 | 20 | 40 |
故有85%的把握认为性别与是否喜欢数学课程有关系;
(2)设该班另外4名喜欢数学的女同学为B,C,D,E,从该班喜欢数学的女生中随机抽取2人有AB,AC,AD,AE,BC,BD,BE,CD,CE,DE,共10种方法,符号条件:女生A被选中的情形有AB,AC,AD,AE,共4种,
故女生A被选中的概率为$\frac{4}{10}$=$\frac{2}{5}$.
点评 本题考查独立性检验的应用,考查概率的计算,本题解题的关键是正确利用观测值公式求出观测值.

练习册系列答案
相关题目
12.为了调查中学生近视情况,某校150名男生中有80名近视,140名女生中有70名近视,在检验这些中学生眼睛近视是否与性别有关时用什么方法最有说服力( )
| A. | 平均数 | B. | 方差 | C. | 回归分析 | D. | 独立性检验 |
 .
.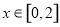 时,函数
时,函数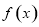 恒有意义,求实数
恒有意义,求实数 的取值范围;
的取值范围; ,使得函数
,使得函数 在区间
在区间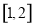 上为减函数,并且最大值为1?如果存在?试求出
上为减函数,并且最大值为1?如果存在?试求出 的值;如果不存在,请说明理由.
的值;如果不存在,请说明理由.


