题目内容
8.已知函数f(x)=lnx-$\frac{1}{2}$x2,g(x)=$\frac{1-m}{2}$x2+x,m∈R,令F(x)=f(x)+g(x).(Ⅰ)求函数f(x)的单调递增区间;
(Ⅱ)若关于x的不等式F(x)≤mx-1恒成立,求整数m的最小值;
(Ⅲ)若m=-1,且正实数x1,x2满足F(x1)=-F(x2),求证:x1+x2$≥\sqrt{3}$-1.
分析 (Ⅰ)先求出函数的导数,从而得到函数的单调区间;
(Ⅱ)令G(x)=F(x)-(mx-1)=lnx-$\frac{1}{2}$mx2+(1-m)x+1,则不等式F(x)≤mx-1恒成立,即G(x)≤0恒成立,通过讨论G(x)的单调性,从而求出m的范围;
(Ⅲ)将m=-1代入函数表达式,得到关于x1,x2的方程,令t=x1•x2>0,则由φ(t)=t-lnt,通过讨论函数的单调性,从而证出结论.
解答 解:(Ⅰ)f(x)的定义域为:{x|x>0},
f′(x)=$\frac{1}{x}$-x=$\frac{1{-x}^{2}}{x}$,(x>0),
由f′(x)>0,得:0<x<1,
所以f(x)的单调递增区间为(0,1).
(Ⅱ)F(x)=f(x)+g(x)=lnx-$\frac{1}{2}$mx2+x,x>0,
令G(x)=F(x)-(mx-1)=lnx-$\frac{1}{2}$mx2+(1-m)x+1,
则不等式F(x)≤mx-1恒成立,即G(x)≤0恒成立.
G′(x)=$\frac{1}{x}$-mx+(1-m)=$\frac{-{mx}^{2}+(1-m)x+1}{x}$,
①当m≤0时,因为x>0,所以G′(x)>0
所以G(x)在(0,+∞)上是单调递增函数,
又因为G(1)=ln1-$\frac{1}{2}$m×12+(1-m)+1=-$\frac{3}{2}$m+2>0,
所以关于x的不等式G(x)≤0不能恒成立,
②当m>0时,G′(x)=-$\frac{m(x-\frac{1}{m})(x-1)}{x}$,
令G′(x)=0,因为x>0,得x=$\frac{1}{m}$,
所以当x∈(0,$\frac{1}{m}$)时,G′(x)>0;当x∈($\frac{1}{m}$,+∞)时,G′(x)<0,
因此函数G(x)在x∈(0,$\frac{1}{m}$)是增函数,在x∈($\frac{1}{m}$,+∞)是减函数,
故函数G(x)的最大值为:
G($\frac{1}{m}$)=ln$\frac{1}{m}$-$\frac{1}{2}$m×${(\frac{1}{m})}^{2}$+(1-m)×$\frac{1}{m}$+1=$\frac{1}{2m}$-lnm,
令h(m)=$\frac{1}{2m}$-lnm,因为h(m)在m∈(0,+∞)上是减函数,
又因为h(1)=$\frac{1}{2}$>0,h(2)=$\frac{1}{4}$-ln2<0,所以当m≥2时,h(m)<0,
所以整数m的最小值为2.
(Ⅲ)m=-1时,F(x)=lnx+$\frac{1}{2}$x2+x,x>0,
由F(x1)=-F(x2),得F(x1)+F(x2)=0,即lnx1+$\frac{1}{2}$${{x}_{1}}^{2}$+x1+lnx2+$\frac{1}{2}$${{x}_{2}}^{2}$+x2=0,
整理得:$\frac{1}{2}$${{(x}_{1}{+x}_{2})}^{2}$+(x1+x2)=x1 x2-ln(x1 x2),
令t=x1•x2>0,则由φ(t)=t-lnt,得:φ′(t)=$\frac{t-1}{t}$,
可知φ(t)在区间(0,1)上单调递减,在区间(1,+∞)上单调递增,
所以φ(t)≥φ(1)=1,
所以$\frac{1}{2}$${{(x}_{1}{+x}_{2})}^{2}$+(x1+x2)≥1,解得:x1+x2≤-$\sqrt{3}$-1,或x1+x2≥$\sqrt{3}$-1,
因为x1,x2为正整数,所以:x1+x2≥$\sqrt{3}$-1成立.
点评 本题考查了函数的单调性问题,考查函数恒成立问题,考查导数的应用,是一道难题.

 下图是1,2两组各7名同学体重(单位:千克)数据的茎叶图.设1,2两组数据的平均数依次为$\overline{x_1}$和$\overline{x_2}$,标准差依次为s1和s2,那么( )
下图是1,2两组各7名同学体重(单位:千克)数据的茎叶图.设1,2两组数据的平均数依次为$\overline{x_1}$和$\overline{x_2}$,标准差依次为s1和s2,那么( )(注:标准差s=$\sqrt{\frac{1}{n}[{{({x_1}-\overline x)}^2}+{{({x_2}-\overline x)}^2}+…+{{({x_n}-\overline x)}^2}}$,其中$\overline{x_1}$为x1,x2,…,xn的平均数)
| A. | $\overline{x_1}$<$\overline{x_2}$,s1<s2 | B. | $\overline{x_1}$<$\overline{x_2}$,s1>s2 | C. | $\overline{x_1}$>$\overline{x_2}$,s1>s2 | D. | $\overline{x_1}$>$\overline{x_2}$,s1<s2 |
| A. | a,b,c成等比数列 | B. | a,b,c成等差数列 | C. | 1+2cos2B≥0 | D. | S≤$\frac{\sqrt{3}}{4}$(a2+c2-b2) |
| A. | 2 | B. | $\root{3}{4}$ | C. | $\frac{\sqrt{2}}{4}$ | D. | 1 |
①(1,+∞)是f(x)的单调递减区间;
②当k∈(-∞,$\frac{1}{e}$)时,直线y=k与y=f(x)的图象有两个不同交点;
③函数y=f(x)的图象与y=x2+1的图象没有公共点.
其中正确结论的序号是( )
| A. | ①②③ | B. | ①③ | C. | ①② | D. | ②③ |
| A. | a<-1或a>3 | B. | -1<a<3 | C. | -1<a<2 | D. | 1<a<3 |
| A. | 6 | B. | 12 | C. | 18 | D. | 25 |
 对某班40名高中学生是否喜欢数学课程进行问卷调查,将调查所得数据绘制成二维条形图如图所示.
对某班40名高中学生是否喜欢数学课程进行问卷调查,将调查所得数据绘制成二维条形图如图所示.(Ⅰ)根据图中相关数据完成以下2×2列联表,并计算有多大把握认为性别与是否喜欢数学有关系?
| 喜欢数学课程 | 不喜欢数学课程 | 总计 | |
| 男 | |||
| 女 | |||
| 总计 | 40 |
参考公式:K2=$\frac{(a+b+c+d)(ad-bc)^{2}}{(a+b)(c+d)(a+c)(b+d)}$.
临界值附表:
| P(K2≥k0) | 0.5 | 0.4 | 0.25 | 0.15 | 0.1 | 0.01 |
| k0 | 0.455 | 0.708 | 1.323 | 2.072 | 2.706 | 6.635 |
 则下列结论正确的是( )
则下列结论正确的是( ) 是偶函数 B.
是偶函数 B. 是增函数
是增函数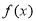 是周期函数 D.
是周期函数 D. 的值域为
的值域为