题目内容
2.在Rt△ABC中,∠C=90°,当n>2时,有cn>an+bn成立,请你类比直角三角形的这个性质,猜想一下空间四面体的性质.分析 线的关系类比到面的关系,即可得出结论.
解答 解:线的关系类比到面的关系,在空间四面体ABCD中,
猜测:S△BCD2=S△ABC2+S△ACD2+S△ADB2.理由如下: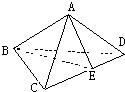
如图作AE⊥CD连BE,则BE⊥CD.
S△BCD2 =$\frac{1}{4}$CD2•BE2 =$\frac{1}{4}$CD2(AB2+AE2)
=$\frac{1}{4}$(AC2+AD2)(AB2+AE2)
=$\frac{1}{4}$(AC2AB2 +AD2AB2 +AC2AE2+AD2AE2 )
=$\frac{1}{4}$(AC2AB2 +AD2AB2+CD2AE2 )
=S△ABC2+S△ACD2+S△ADB2
点评 本题考查类比推理,体现了数形结合的数学思想.其中由二维到三维的类比推理要注意点的性质往往推广为线的性质,线的性质往往推广为面的性质.

练习册系列答案
相关题目
3.已知函数f(x)=$\frac{x}{{e}^{x}}$,给出下列结论:
①(1,+∞)是f(x)的单调递减区间;
②当k∈(-∞,$\frac{1}{e}$)时,直线y=k与y=f(x)的图象有两个不同交点;
③函数y=f(x)的图象与y=x2+1的图象没有公共点.
其中正确结论的序号是( )
①(1,+∞)是f(x)的单调递减区间;
②当k∈(-∞,$\frac{1}{e}$)时,直线y=k与y=f(x)的图象有两个不同交点;
③函数y=f(x)的图象与y=x2+1的图象没有公共点.
其中正确结论的序号是( )
| A. | ①②③ | B. | ①③ | C. | ①② | D. | ②③ |
7. 对某班40名高中学生是否喜欢数学课程进行问卷调查,将调查所得数据绘制成二维条形图如图所示.
对某班40名高中学生是否喜欢数学课程进行问卷调查,将调查所得数据绘制成二维条形图如图所示.
(Ⅰ)根据图中相关数据完成以下2×2列联表,并计算有多大把握认为性别与是否喜欢数学有关系?
(Ⅱ)从该班喜欢数学的女生中随机选取2人,参加学校数学兴趣课程班,已知该班女生A喜欢数学课程,求女生A被选中的概率.
参考公式:K2=$\frac{(a+b+c+d)(ad-bc)^{2}}{(a+b)(c+d)(a+c)(b+d)}$.
临界值附表:
 对某班40名高中学生是否喜欢数学课程进行问卷调查,将调查所得数据绘制成二维条形图如图所示.
对某班40名高中学生是否喜欢数学课程进行问卷调查,将调查所得数据绘制成二维条形图如图所示.(Ⅰ)根据图中相关数据完成以下2×2列联表,并计算有多大把握认为性别与是否喜欢数学有关系?
| 喜欢数学课程 | 不喜欢数学课程 | 总计 | |
| 男 | |||
| 女 | |||
| 总计 | 40 |
参考公式:K2=$\frac{(a+b+c+d)(ad-bc)^{2}}{(a+b)(c+d)(a+c)(b+d)}$.
临界值附表:
| P(K2≥k0) | 0.5 | 0.4 | 0.25 | 0.15 | 0.1 | 0.01 |
| k0 | 0.455 | 0.708 | 1.323 | 2.072 | 2.706 | 6.635 |
14.一个机器人每一秒钟前进一步或后退一步,程序设计师设计的程序是让机器人以先前进3步,然后再后退2步的规律移动.如果将机器人放在数轴的原点,面向正的方向在数轴上移动(1步的距离为1个单位长度).令P(n)表示第n秒时机器人所在位置的坐标,且记P(0)=0,则下列结论中错误的是( )
| A. | P(3)=3 | B. | P(5)=1 | C. | P(2007)>P(2006) | D. | P(2003)<P(2006) |
10.曲线y=$\frac{1}{3}$x3在点(1,$\frac{1}{3}$)处的切线与直线x+y-3=0的夹角为( )
| A. | 30° | B. | 45° | C. | 60° | D. | 90° |
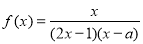 为奇函数,则
为奇函数,则 的值为( )
的值为( ) B.
B.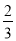 C.
C. D.
D.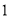
 ,则
,则 的大小关系是( )
的大小关系是( ) B.
B.
 D.
D.
 ,则
,则 ( )
( ) B.
B. C.
C. D.
D.