题目内容
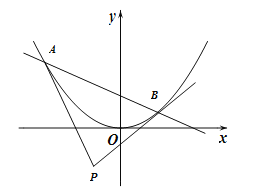
【题目】双曲线 
﹣ 
=1（a＞0，b＞0）的左、右焦点分别为F1 ， F2 ， P为双曲线上一点，且 
=0，△F1PF2的内切圆半径r=2a，则双曲线的离心率e= ．
【答案】5
【解析】解：可设P为第一象限的点，
由双曲线的定义可得|PF1|﹣|PF2|=2a，①
=0，可得PF1⊥PF2 ，
由勾股定理可得|PF1|2+|PF2|2=|F1F2|2=4c2 ， ②
②﹣①2 ， 可得2|PF1||PF2|=4c2﹣4a2=4b2 ，
即有|PF1|+|PF2|= 
，
由三角形的面积公式可得 
r（|PF1|+|PF2|+|F1F2|）= |PF1||PF2|，
即为2a（ +2c）=2b2 ，
即有c+2a= 
，两边平方可得
c2+4a2+4ac=c2+b2=c2+c2﹣a2 ，
即c2﹣4ac﹣5a2=0，解得c=5a（c=﹣a舍去），
即有e= 
=5．
所以答案是：5．
练习册系列答案
步步高达标卷系列答案
相关题目
