题目内容
【题目】已知直线![]() :
: ![]() 与抛物线
与抛物线![]() 交于
交于![]() ,
, ![]() 两点,记抛物线在
两点,记抛物线在![]() ,
, ![]() 两点处的切线
两点处的切线![]() ,
, ![]() 的交点为
的交点为![]() .
.
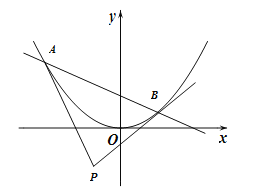
(I)求证: ![]() ;
;
(II)求点![]() 的坐标(用
的坐标(用![]() ,
, ![]() 表示);
表示);
(Ⅲ)若![]() ,求△
,求△![]() 的面积的最小值.
的面积的最小值.
【答案】(Ⅰ)见解析 (Ⅱ) ![]() (III)
(III)![]()
【解析】试题分析:(Ⅰ) 由![]() ,可得
,可得![]() ,根据韦达定理可得结果;(Ⅱ) 设
,根据韦达定理可得结果;(Ⅱ) 设![]() :
: ![]() ,由
,由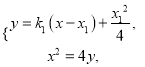 联立可得
联立可得![]() ,解得
,解得![]() ,可得以
,可得以![]() :
: ![]() ,同理可得
,同理可得![]() :
: ![]() ,两式联立可解得点
,两式联立可解得点![]() 的坐标;(Ⅲ)根据弦长公式、点到直线距离公式以及三角形面积公式,可得
的坐标;(Ⅲ)根据弦长公式、点到直线距离公式以及三角形面积公式,可得![]() ,由
,由![]() 得
得![]() ,
, ![]() ,化简后利用基本不等式可得结果.
,化简后利用基本不等式可得结果.
试题解析:(Ⅰ) 解:由![]()
可得![]() ,
,
所以![]() ,
, ![]() .
.
(Ⅱ) 证明:由已知![]() ,所以可设
,所以可设![]() :
: ![]() ,由
,由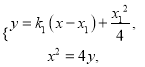 联立可得
联立可得![]() ,由
,由![]() ,所以
,所以![]() . 所以
. 所以![]() :
: ![]() ,同理可得
,同理可得![]() :
: ![]() . 由
. 由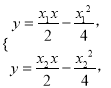 解得
解得![]() ,
, ![]() ,
,
所以点![]() 的坐标为
的坐标为![]() .
.
(III)由(Ⅱ)可知点![]()
![]() 到直线
到直线![]() 的距离
的距离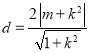 ,又
,又![]() ,所以△
,所以△![]() 的面积
的面积![]() .
.
因为![]() ,
, ![]() ,所以
,所以![]() ,当
,当![]() ,
, ![]() 取到等号,所以△
取到等号,所以△![]() 的面积的最小值为
的面积的最小值为![]() .
.

练习册系列答案
 提分百分百检测卷系列答案
提分百分百检测卷系列答案 宝贝计划期末冲刺夺100分系列答案
宝贝计划期末冲刺夺100分系列答案 能考试全能100分系列答案
能考试全能100分系列答案
相关题目
【题目】某综艺节目为增强娱乐性,要求现场嘉宾与其场外好友连线互动.凡是拒绝表演节目的好友均无连线好友的机会;凡是选择表演节目的好友均需连线未参加过此活动的3个好友参与此活动,以此下去.
(Ⅰ)假设每个人选择表演与否是等可能的,且互不影响,则某人选择表演后,其连线的3个好友中不少于2个好友选择表演节目的概率是多少?
(Ⅱ)为调查“选择表演者”与其性别是否有关,采取随机抽样得到如表:
选择表演 | 拒绝表演 | 合计 | |
男 | 50 | 10 | 60 |
女 | 10 | 10 | 20 |
合计 | 60 | 20 | 80 |
①根据表中数据,是否有99%的把握认为“表演节目”与好友的性别有关?
②将此样本的频率视为总体的概率,随机调查3名男性好友,设X为3个人中选择表演的人数,求X的分布列和期望.
附:K2= ![]() ;
;
P(K2≥k0) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 |
k0 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 |