Question

【题目】定义在（0，+∞）上的函数f（x）=a（x+ ）﹣|x﹣ |（a∈R）．
（1）当a= 时，求f（x）的单调区间；
（2）若f（x）≥ x对任意的x＞0恒成立，求a的取值范围．

Answer 1

【答案】
（1）解：当a= 时，f（x）= ，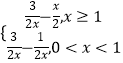

当x≥1时，f（x）= ﹣ 的导数为f′（x）=﹣ ﹣ ＜0；

当0＜x＜1时，f（x）= ﹣ 的导数为f′（x）= + ＞0；

所以f（x）的单调递增区间是（0，1]，单调递减区间是[1，+∞）．

（2）解：由f（x）≥ x得a（x+ ）﹣|x﹣ |≥ x，x＞0，

可得a（x2+1）﹣|x2﹣1|≥ x2，

①当0＜x＜1时，a（x2+1）+（x2﹣1）≥ x2，

即有a≥ ，

由 = ﹣ ∈（ ，1）

可得a≥1；

②当x≥1时，a（x2+1）﹣（x2﹣1）≥ x2，

可得a≥

由 = ﹣ ∈[ ， ）

可得a≥ ．

综上所述，a的取值范围是[ ，+∞）．

【解析】（1）求出a= 时，讨论当x≥1时，当0＜x＜1时，去掉绝对值，求得导数，判断符号，即可得到所求单调区间；（2）由f（x）≥ x可得a（x2+1）﹣|x2﹣1|≥ x2 ， 讨论当0＜x＜1时，当x≥1时，运用参数分离和函数的单调性可得最值，进而得到a的范围．