题目内容
【题目】如图，将宽和长都分别为x，
的两个矩形部分重叠放在一起后形成的正十字形面积为
注：正十字形指的是原来的两个矩形的顶点都在同一个圆上，且两矩形长所在的直线互相垂直的图形
，
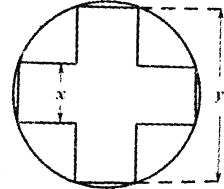
求y关于x的函数解析式；
当x，y取何值时，该正十字形的外接圆面积最小，并求出其最小值．
【答案】(1)
；(2)当且仅当
，
时，外接圆面积最小，且最小值为
.
【解析】
根据几何图形的面积即可得到函数的解析式，并求出函数的定义域，
设正十字形的外接圆的直径为d，由图可知
，利用基本不等式求出d的最小值，可得半径最小值，则正十字形的外接圆面积最小值可求．
由题意可得：
，则
，
，
，解得
．
关于x的解析式为
；
设正十字形的外接圆的直径为d，
由图可知
，
当且仅当
，
时，正十字形的外接圆直径d最小，
最小为
，则半径最小值为
，
正十字形的外接圆面积最小值为
．
练习册系列答案
每日10分钟口算心算速算天天练系列答案
相关题目
