题目内容
【题目】在平面直角坐标系![]() 中,动直线
中,动直线![]() 交抛物线
交抛物线![]() 于A,B两点.
于A,B两点.
(1)若![]() ,证明直线
,证明直线![]() 过定点,并求出该定点;
过定点,并求出该定点;
(2)点M为![]() 的中点,过点M作与y轴垂直的直线交抛物线
的中点,过点M作与y轴垂直的直线交抛物线![]() 于C点;点N为
于C点;点N为![]() 的中点,过点N作与y轴垂直的直线交抛物线
的中点,过点N作与y轴垂直的直线交抛物线![]() 于点P.设△
于点P.设△![]() 的面积
的面积![]() ,△
,△![]() 的面积为
的面积为![]() .
.
(i)若![]() 过定点
过定点![]() ,求使
,求使![]() 取最小值时,直线
取最小值时,直线![]() 的方程;
的方程;
(ii)求![]() 的值.
的值.
【答案】(1)证明见解析;定点![]() (2)(i)
(2)(i)![]() (ii)
(ii)![]()
【解析】
(1)设直线![]() 的方程,并代入抛物线方程,利用韦达定理和
的方程,并代入抛物线方程,利用韦达定理和![]() 可解决;
可解决;
(2)(i)得到![]() 、
、![]() 的坐标,得到
的坐标,得到![]() ,进而得到
,进而得到![]() ,再根据二次函数可求得最小值;(ii)求出
,再根据二次函数可求得最小值;(ii)求出![]() ,求出
,求出![]() 代入
代入![]() 即可得到结果.
即可得到结果.
(1)证明:依题意可设直线![]() 的方程为
的方程为![]() ,
,
代入![]() 消去x得:
消去x得:![]() ,
,
![]() ,即
,即![]() ,
,
设![]() ,
,![]() ,则
,则![]() ,
,![]() ,
,
因为![]() ,所以
,所以![]() ,
,
又![]() ,
,![]() ,所以
,所以![]() ,故
,故![]() ,(
,(![]() 已舍去)
已舍去)
所以![]() ,得
,得![]() ,
,
因此直线![]() 的方程为
的方程为![]() ,该直线过定点
,该直线过定点![]() .
.
(2)(i)因为![]() 过定点
过定点![]() ,所以由(1)得
,所以由(1)得![]() ,即
,即![]() ,
,
![]() 恒成立,
恒成立,![]() ,
,![]() ,
,
由题知得![]() ,
,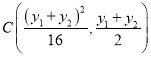 ,
,
所以 ,
,
所以![]() ,
,
因为![]() ,且
,且![]() 时等号成立,
时等号成立,
所以![]() ,
,
当![]() 取到最小值
取到最小值![]() 时,
时,![]() ,
,![]() ,
,
直线![]() 的方程为
的方程为![]() ,即
,即![]() .
.
(ii)依题知可得![]() ,
,![]() ,
,
所以![]() ,
,
由(2)(i)可知![]() (此处
(此处![]() 可以理解为A,B两点的纵向高度差)
可以理解为A,B两点的纵向高度差)
同理可得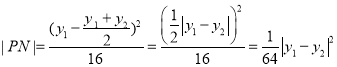 ,
,
所以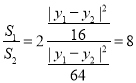 .
.

练习册系列答案
相关题目