题目内容
【题目】圆周率π是数学中一个非常重要的数,历史上许多中外数学家利用各种办法对π进行了估算.现利用下列实验我们也可对圆周率进行估算.假设某校共有学生N人,让每人随机写出一对小于1的正实数a,b,再统计出a,b,1能构造锐角三角形的人数M,利用所学的有关知识,则可估计出π的值是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
【答案】B
【解析】
首先求出0<a<1,0<b<1,构成的区域面积,然后利用余弦定理求出满足是锐角三角形所构成的区域,然后利用几何概型—面积比即可求解.
学校共有学生N人,每人随机写出一对小于1的正实数a,b,
得到N个实数对(a,b),
因为0<a<1,0<b<1,所以N个实数对(a,b)都在边长为1的正方形AOBC内,
如图所示:
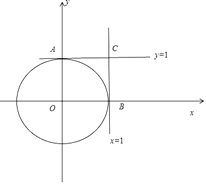
若a,b,1能构造锐角三角形,因为1是最长边,所以1所对的角为锐角,
所以![]() ,
,![]() ,即a2+b2>1,
,即a2+b2>1,![]()
所以N对实数对落在单位圆x2+y2=1外的有M对,
由几何概率的概率公式可得: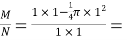
![]() ,
,
所以π![]() ,
,
故选:B.

练习册系列答案
 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案
相关题目