题目内容
3.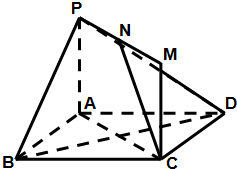 如图,矩形ACMP和菱形ABCD所在的平面互相垂直,点N为PM的中点,
如图,矩形ACMP和菱形ABCD所在的平面互相垂直,点N为PM的中点,(1)证明:直线CN∥平面PBD
(2)若AP=AB,∠BAD=120°,求直线MC与平面PBD所成角的正切值.
分析 (1)连结AC、BD,交于点O,连结OP,通过四边形OCNP为平行四边形,及线面平行的判定定理即得结论;
(2)易得∠MCN即为直线MC与平面PBD所成角的平面角.在Rt△MCN中,利用tan∠MCN=$\frac{MN}{MC}$计算即可.
解答  (1)证明:连结AC、BD,交于点O,连结OP,
(1)证明:连结AC、BD,交于点O,连结OP,
则O为AC的中点,
又∵四边形ACMP为矩形,点N为PM的中点,
∴PN∥OC,PN=OC,
∴四边形OCNP为平行四边形,
∴NC∥OP,
∴直线CN∥平面PBD;
(2)解:根据题意易得∠MCN即为直线MC与平面PBD所成角的平面角.
∵AP=AB,∠BAD=120°,
∴AC=AB=PA,
又由(1)可得MN=$\frac{1}{2}$AC,MC=AC,
∴在Rt△MCN中,tan∠MCN=$\frac{MN}{MC}$=$\frac{1}{2}$.
点评 本题考查空间中线面平行的判定,考查求线面角的三角函数值,注意解题方法的积累,属于中档题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
3.已知随机变量ξ~N(0,σ2),若P(ξ>3)=0.023,则P(-3≤ξ≤3)=( )
| A. | 0.477 | B. | 0.628 | C. | 0.954 | D. | 0.977 |
13.以坐标原点O为顶点,x轴的正半轴为始边,角α,β,θ的终边分别为OA,OB,OC,OC为∠AOB的角平分线,若$tanθ=\frac{1}{3}$,则tan(α+β)=( )
| A. | $\frac{1}{4}$ | B. | $\frac{1}{3}$ | C. | $\frac{2}{3}$ | D. | $\frac{3}{4}$ |