题目内容
(本小题满分12分)
已知椭圆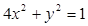 及直线
及直线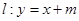 ,当直线和椭圆有公共点时.
,当直线和椭圆有公共点时.
(1)求实数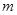 的取值范围;
的取值范围;
(2)求被椭圆截得的最长的弦所在的直线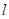 的方程.
的方程.
已知椭圆
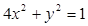 及直线
及直线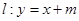 ,当直线和椭圆有公共点时.
,当直线和椭圆有公共点时.(1)求实数
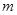 的取值范围;
的取值范围;(2)求被椭圆截得的最长的弦所在的直线
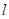 的方程.
的方程. (1)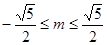 ; (2) y=x
; (2) y=x
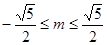 ; (2) y=x
; (2) y=x试题分析:(1)直线与椭圆有公共点,说明它们的方程组成的方程组有解,因而它们的方程联立消去y后得到关于x的一元二次方程的判别式大于或等于零,从而得到m的取值范围.
(2)在(1)的基础上利用弦长公式
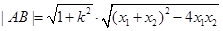 得到关于m的函数关系式,再利用函数的方法求最值即可,事实上应该是直线y=x+m过椭圆中心时弦长最长.
得到关于m的函数关系式,再利用函数的方法求最值即可,事实上应该是直线y=x+m过椭圆中心时弦长最长.点评:(1)直线与椭圆的位置关系可利用它们组成的方程组的公共解的个数来判断,当没有公共解时,此时
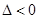 ,直线与椭圆相离;当有一个公共点时,此时
,直线与椭圆相离;当有一个公共点时,此时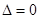 ,直线与椭圆相切;当有两个公共点时,此时
,直线与椭圆相切;当有两个公共点时,此时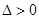 ,直线与椭圆相交.
,直线与椭圆相交.(2)当相交涉及最值时一般要利用韦达定理及判别式建立关于参数的函数关系式,从函数的角度求最值.

练习册系列答案
相关题目
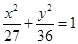 有相同焦点,且经过点(
有相同焦点,且经过点(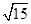 ,4),求其方程.
,4),求其方程.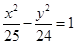 上的点
上的点 到一个焦点的距离为11,则它到另一个焦点的距离为( )
到一个焦点的距离为11,则它到另一个焦点的距离为( )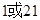
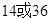
 是曲线
是曲线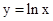 的切线,则
的切线,则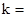 。
。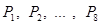 是抛物线
是抛物线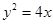 上的点,它们的横坐标依次为
上的点,它们的横坐标依次为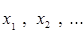
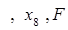 是抛物线的焦点,若
是抛物线的焦点,若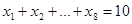 ,则
,则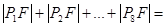 _______________.
_______________.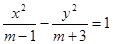 表示双曲线,则实数
表示双曲线,则实数 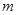 的取值范围是( )
的取值范围是( )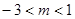
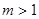
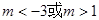
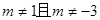
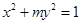 的离心率为
的离心率为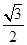 ,则它的长半轴长为_______
,则它的长半轴长为_______