题目内容
6.已知向量$\overrightarrow{a}$=(2,-2),$\overrightarrow{b}$=(5,k).若|$\overrightarrow{b}$-$\overrightarrow{a}$|不超过5,则k的取值范围是[-6,2].分析 先求出$\overrightarrow{b}-\overrightarrow{a}=(3,k+2)$,从而得到$\sqrt{9+(k+2)^{2}}≤5$,解该不等式即可得出k的取值范围.
解答 解:$\overrightarrow{b}-\overrightarrow{a}=(3,k+2)$;
$|\overrightarrow{b}-\overrightarrow{a}|≤5$;
∴$\sqrt{{3}^{2}+(k+2)^{2}}≤5$;
∴(k+2)2≤16;
∴-4≤k+2≤4;
∴-6≤k≤2;
∴k的取值范围是[-6,2].
故答案为:[-6,2].
点评 考查向量坐标的减法运算,根据向量的坐标求向量长度,解无理不等式.

练习册系列答案
相关题目
16.已知命题p:?x∈R,x-2>lgx,命题q:?x∈R,ex>1,则( )
| A. | 命题p∨q是假命题 | B. | 命题p∧q是真命题 | ||
| C. | 命题p∧(?q)是假命题 | D. | 命题p∨(?q)是真命题 |
14.已知实数a,b,则“2a>2b”是“log2a>log2b”的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
15.如果方程x2+(m-1)x+m2-2=0的两个实根一个小于-1,另一个大于1,那么实数m的取值范围是( )
| A. | -$\sqrt{2}$<m<$\sqrt{2}$ | B. | -2<m<0 | C. | -2<m<1 | D. | 0<m<1 |
16.计算定积分${∫}_{0}^{2}$($\sqrt{2x-{x}^{2}}$+x)dx( )
| A. | $\frac{π}{2}$+4 | B. | π+2 | C. | $\frac{π}{2}$+2 | D. | π+4 |
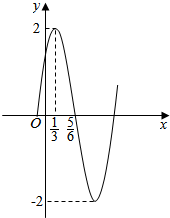 已知函数f(x)=Asin(ωx+ϕ)(A>0,?>0,|ϕ|<$\frac{π}{2}$)的部分图象如图所示,则函数f(x)的解析式为y=2sin(πx+$\frac{π}{6}$).
已知函数f(x)=Asin(ωx+ϕ)(A>0,?>0,|ϕ|<$\frac{π}{2}$)的部分图象如图所示,则函数f(x)的解析式为y=2sin(πx+$\frac{π}{6}$).