题目内容
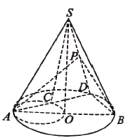
【题目】如图,![]() 是圆锥
是圆锥![]() 的底面
的底面![]() 的直径,
的直径,![]() 是圆
是圆![]() 上异于
上异于![]() 的任意一点,以
的任意一点,以![]() 为直径的圆与
为直径的圆与![]() 的另一个交点为
的另一个交点为![]() 为
为![]() 的中点.现给出以下结论:
的中点.现给出以下结论:
①![]() 为直角三角形
为直角三角形
②平面![]() 平面
平面![]()
③平面![]() 必与圆锥
必与圆锥![]() 的某条母线平行
的某条母线平行
其中正确结论的个数是
A. 0B. 1C. 2D. 3
【答案】C
【解析】
①根据线面垂直的判定定理证明AC⊥平面SOC即可
②假设平面SAD⊥平面SBD,根据面面垂直的性质定理推出矛盾即可
③连接DO并延长交圆于E,连接PO,SE,利用中位线的性质进行判断即可
①∵SO⊥底面圆O,
∴SO⊥AC,
C在以AO为直径的圆上,
∴AC⊥OC,
∵OC∩SO=O,
∴AC⊥平面SOC,AC⊥SC,
即①△SAC为直角三角形正确,故①正确,
②假设平面SAD⊥平面SBD,在平面SAD中过A作AH⊥SD交SD于H,则AH⊥平面SBD,∴AH⊥BD,
又∵BD⊥AD,∴BD⊥面SAD,又CO∥BD,∴CO⊥面SAD,∴CO⊥SC,又在△SOC中,SO⊥OC,在一个三角形内不可能有两个直角,故平面SAD⊥平面SBD不成立,故②错误,
③连接DO并延长交圆于E,连接PO,SE,
∵P为SD的中点,O为ED的中点,
∴OP是△SDE的中位线,
∴PO∥SE,
即SE∥平面APB,
即平面PAB必与圆锥SO的母线SE平行.故③正确,
故正确是①③,
故选:C.

【题目】商品的销售价格与销售量密切相关,为更精准地为商品确定最终售价,商家对商品A按以下单价进行试售,得到如下数据:
单价x(元) | 15 | 16 | 17 | 18 | 19 |
销量y(件) | 60 | 58 | 55 | 53 | 49 |
(1)求销量y关于x的线性回归方程;
(2)预计今后的销售中,销量与单价服从(1)中的线性回归方程,已知每件商品A的成本是10元,为了获得最大利润,商品A的单价应定为多少元?(结果保留整数)
(附: ,
,![]() .(15×60+16×58+17×55+18×53+19×49=4648,152+162+172+182+192=1455)
.(15×60+16×58+17×55+18×53+19×49=4648,152+162+172+182+192=1455)