题目内容
【题目】圆![]() 与
与![]() 轴交于
轴交于![]() 、
、![]() 两点,
两点,![]() 为圆上一点.椭圆
为圆上一点.椭圆![]() 以
以![]() 、
、![]() 为焦点且过点
为焦点且过点![]() .
.
(Ⅰ)当![]() 点坐标为
点坐标为![]() 时,求
时,求![]() 的值及椭圆方程;
的值及椭圆方程;
(Ⅱ)若直线![]() 与(Ⅰ)中所求的椭圆交于
与(Ⅰ)中所求的椭圆交于![]() 、
、![]() 不同的两点,且点
不同的两点,且点![]() ,
,![]() ,求直线
,求直线![]() 在
在![]() 轴上截距
轴上截距![]() 的取值范围.
的取值范围.
【答案】(Ⅰ)![]() ,椭圆方程为
,椭圆方程为![]() ;(Ⅱ)当
;(Ⅱ)当![]() 时,直线
时,直线![]() 在
在![]() 轴上的截距的取值范围是
轴上的截距的取值范围是![]() ;当
;当![]() 时,直线
时,直线![]() 在
在![]() 轴上的截距的取值范围是
轴上的截距的取值范围是![]() .
.
.
【解析】
(Ⅰ)由圆与![]() 轴的交点为
轴的交点为![]() 得椭圆的焦距
得椭圆的焦距![]() ,从而椭圆方程化为
,从而椭圆方程化为![]() ,将
,将![]() 代入圆,能求出
代入圆,能求出![]() ,从而
,从而![]() ,由此能求出
,由此能求出![]() ,进而能求出椭圆方程.
,进而能求出椭圆方程.
(Ⅱ)由![]() ,得点
,得点![]() 在线段
在线段![]() 的中垂线上,当
的中垂线上,当![]() 时,
时,![]() 与椭圆交于两点都满足题意,从而
与椭圆交于两点都满足题意,从而![]() ;当
;当![]() 时,设
时,设![]() ,
,![]() ,中点
,中点![]() ,由
,由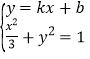 ,得
,得![]() ,由
,由![]() ,得
,得![]() ,再利用点差法能求出结果.
,再利用点差法能求出结果.
(Ⅰ)由圆与![]() 轴的交点为
轴的交点为![]() 得椭圆的焦距
得椭圆的焦距![]()
![]()
![]()
![]() 椭圆方程化为
椭圆方程化为![]() ……①
……①
将![]() 代入圆,得
代入圆,得![]()
![]()
![]() 代入①式,得
代入①式,得![]()
解得![]()
![]() 椭圆方程为
椭圆方程为![]()
(Ⅱ)由![]() ,得点
,得点![]() 应该在线段
应该在线段![]() 的中垂线上
的中垂线上
当![]() 时,
时,![]() 与椭圆交于两点都满足题意
与椭圆交于两点都满足题意 ![]()
当![]() 时,设
时,设![]() ,
,![]() ,中点
,中点![]()
由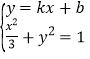 ,消
,消![]() 得
得![]()
由![]() ,得
,得![]() ……②
……②
由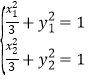 ,作差,得
,作差,得![]()
由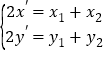 ,及
,及![]() ,得
,得![]() ……③
……③
![]()
![]() ……④
……④
由③④得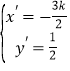 ,代入
,代入![]() 中,得
中,得![]() ……⑤
……⑤
将⑤式代入②式,得![]()
由⑤得![]() ,得
,得![]()
![]() 的取值范围是
的取值范围是![]()
综上,当![]() 时,直线
时,直线![]() 在
在![]() 轴上的截距的取值范围是
轴上的截距的取值范围是![]() ;
;
当![]() 时,直线
时,直线![]() 在
在![]() 轴上的截距的取值范围是
轴上的截距的取值范围是![]() .
.

练习册系列答案
相关题目