题目内容
【题目】已知函数![]() ,
,![]() .
.
(I)讨论![]() 的单调性;
的单调性;
(II)若![]() 恒成立,证明:当
恒成立,证明:当![]() 时,
时,![]() .
.
(III)在(II)的条件下,证明:![]() .
.
【答案】I.见解析;Ⅱ.见解析;III 见解析.
【解析】
I:对函数求导,分类讨论导函数的正负,进而得到单调性;Ⅱ:通过分类讨论可得到a=1,根据![]() ,得到:
,得到:![]() ,进而得到结果; III:通过讨论函数的单调性得到
,进而得到结果; III:通过讨论函数的单调性得到![]() ,进而得到:
,进而得到:![]() ,由Ⅱ知
,由Ⅱ知![]() 两式相乘得到结果.
两式相乘得到结果.
I.![]()
若![]() ,f(x)在
,f(x)在![]() 上递增;
上递增;
若a>0,当![]() 时,
时,![]() ,f(x)单调递增;
,f(x)单调递增;
当![]() 时,
时,![]() 单调递减。
单调递减。
Ⅱ.由I知,若a≤0,f(x)在(0,+![]() )上递增,又f(l)=0,故f(x)≤0不恒成立
)上递增,又f(l)=0,故f(x)≤0不恒成立
若a>1,当![]() 时,f(x)递减,f(x)>f(1)=0,不合题意。
时,f(x)递减,f(x)>f(1)=0,不合题意。
若0<a<1,当![]() 时,f(x)递增,f(x)>f(l)=0.不合题意。
时,f(x)递增,f(x)>f(l)=0.不合题意。
若a=1.f(x)在(0,1)上递增.在(1,+![]() )上递减,f(x)≤f(1)=0,合题意。
)上递减,f(x)≤f(1)=0,合题意。
故a=1,且![]() (当且仅当x=1时取 “=”)
(当且仅当x=1时取 “=”)
当0<x1<x2时,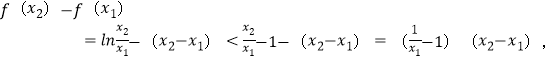
所以![]()
III.![]()
当![]() 时,
时,![]() ,
,![]() 单调递增;
单调递增;
当![]() 时,
时,![]() ,g(x)单调递减。
,g(x)单调递减。
![]()
![]() ①
①
由(Ⅱ)知![]() (当且仅当x=1时取 “=”)........... ②
(当且仅当x=1时取 “=”)........... ②
两个不等式的等号不能同时取到,故得到:
①![]() ②得
②得![]()
即![]() ,
,
![]()

练习册系列答案
相关题目