题目内容
【题目】在平面直角坐标系xOy中，以坐标原点O为极点，x轴正半轴为极轴建立极坐标系，直线l的极坐标方程为ρcosθ+ρsinθ＝1，曲线C的极坐标方程为ρsin2θ＝8cosθ．
（1）求直线l与曲线C的直角坐标方程；
（2）设点M（0，1），直线l与曲线C交于不同的两点P，Q，求|MP|+|MQ|的值．
【答案】（1）直线l的直角坐标方程为x+y＝1，曲线C的直角坐标方程为y2＝8x（2）
【解析】
（1）
代入极坐标方程，即可求解；
（2）把直线方程化为具有几何意义的参数方程，代入曲线C方程，由直线参数的几何意义，即可求解.
（1）直线l的极坐标方程为ρcosθ+ρsinθ＝1，
转换为：x+y＝1，
曲线C的极坐标方程为ρsin2θ＝8cosθ，
转换为：y2＝8x；
（2）考虑直线方程x+y＝1，
则其参数方程为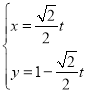
（t为参数），
代入曲线方程y2＝8x，
得到：
，
则有：
．
练习册系列答案
阅读快车系列答案
相关题目
【题目】某单位共有10名员工，他们某年的收入如下表：
员工编号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
年薪（万元） | 4 | 4.5 | 6 | 5 | 6.5 | 7.5 | 8 | 8.5 | 9 | 51 |
（1）求该单位员工当年年薪的平均值和中位数；
（2）已知员工年薪收入与工作年限成正相关关系，某员工工作第一年至第四年的年薪分别为4万元、5.5万元、6万元、8.5万元，预测该员工第六年的年薪为多少？
附：线性回归方程
中系数计算公式分别为：
，
，其中
、
为样本均值.
