${∫} {0}^{1}$x2dx的值为( )A．$\frac{1}{3}$B．1C．$\frac{1}{2}$D．$\frac{2}{3}$ 题目和参考答案——青夏教育精英家教网——

题目内容

17．${∫}_{0}^{1}$x²dx的值为（　　）

A．

$\frac{1}{3}$

B．

1

C．

$\frac{1}{2}$

D．

$\frac{2}{3}$

分析根据定积分的计算法则计算即可．

解答解：${∫}_{0}^{1}$x²dx=$\frac{1}{3}$x³|${\;}_{0}^{1}$=$\frac{1}{3}$，
故选：A．

点评本题考查了定积分的计算，关键是求出原函数，属于基础题．

练习册系列答案

培优新方法系列答案

状元及第系列答案

名师教你学数学系列答案

同步奥数系列答案

高中阶段三测卷系列答案

豫人教育单元检测系列答案

名校名师夺冠王检测卷系列答案

新课堂同步练系列答案

优化方案高中同步测试卷系列答案

上海达标卷系列答案

相关题目

7．函数f（x）=$\frac{2x+1}{{x}^{2}+2}$在区间[0，2]上的最大值是1．

8．已知函数f（x）=2asin（ωx+φ+$\frac{π}{6}$），x∈R，其中（a≠0，ω＞0，0＜φ＜$\frac{π}{2}$），若f（x）的图象相邻两最高点的距离为π，且有一个对称中心为（$\frac{π}{3}$，0）．
（1）求ω和φ的值；
（2）求f（x）的单调递增区间；
（3）若a＞0，试讨论k为何值时，方程f（x）-k=0（x∈[0，a]）有解．

5．在约束条件$\left\{\begin{array}{l}{x+2y≤4}\\{x-y≤1}\\{x+2≥0}\end{array}\right.$下，函数z=3x-y的最小值是（　　）

12．已知△ABC的三个内角A，B，C所对的边分别为a，b，c，向量$\overrightarrow{m}$=（1，2），$\overrightarrow{n}$=（-1，cosA），且$\overrightarrow{m}•\overrightarrow{n}$=0．
（Ⅰ）求角A的大小；
（Ⅱ）若a=$\sqrt{3}$，b+c=2$\sqrt{3}$，求证：△ABC为等边三角形．

如图，函数y=f（x）是可导函数，曲线y=f（x）过点（2，3），且在x=2处的切线l在y轴上的截距为2，令g（x）=xf（x），则曲线y=g（x）在x=2处的切线方程是4x-y-2=0．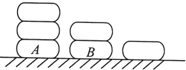

如图，桌面上摆有三串冰糖葫芦，第一串3课，第二串2颗，第三串1颗．小明每次从中取走一颗，若上面的冰糖葫芦取走后才能取下面的冰糖葫芦．则冰糖葫芦A恰好在第五次被取走，且冰糖葫芦B恰好在第六次被取走的取法数为12．

6．已知向量$\overrightarrow{a}$=（$\sqrt{3}$sinx，cosx），$\overrightarrow{b}$=（cosx，cosx），函数f（x）=2$\overrightarrow{a}$•$\overrightarrow{b}$-1
（1）求f（x）的单调递增区间；
（2）当x∈[$\frac{π}{6}$，$\frac{π}{2}$]时，若f（x）=1，求x的值．

12．已知函数f（x）=cos（ωx+θ）为奇函数（0＜θ＜π），其图象与直线y=1的某两个交点的横坐标分别为x₁、x₂，且|x₂-x₁|的最小值为π，则（　　）

$ω=2，θ=\frac{π}{2}$

$ω=\frac{1}{2}，θ=\frac{π}{2}$

$ω=\frac{1}{2}，θ=\frac{π}{4}$

$ω=2，θ=\frac{π}{4}$