题目内容
18.已知函数f(x)=x+$\frac{a}{x}$,g(x)=x-lnx,其中a∈R且a≠0.(Ⅰ) 求曲线y=g(x)在点(1,g(1))处的切线方程;
(II)当a=1时,求函数h(x)=f(x)+g(x)的单调区间;
(III)设函数u(x)=$\left\{{\begin{array}{l}{f(x),f(x)≥g(x)}\\{g(x),f(x)<g(x)}\end{array}}$若u(x)=f(x)对任意x∈[1,e]均成立,求a的取值范围.
分析 (Ⅰ)求出导数,求得切线的斜率和切点,可得切线方程;
(II)求出当a=1时的函数的导数,令导数大于0,求得增区间,令导数小于0,可得减区间,注意定义域;
(III)由题意可得f(x)≥g(x)对任意x∈[1,e]均成立,即为x+$\frac{a}{x}$≥x-lnx,运用参数分离,由导数判断单调性,求得右边函数的最大值,即可得到a的范围.
解答 解:(Ⅰ)g(x)=x-lnx的导数为g′(x)=1-$\frac{1}{x}$,
曲线y=g(x)在点(1,g(1))处的切线斜率为k=g′(1)=0,
切点为(1,1),
则曲线y=g(x)在点(1,g(1))处的切线方程为y=1;
(II)当a=1时,函数h(x)=f(x)+g(x)=2x-lnx+$\frac{1}{x}$,
导数h′(x)=2-$\frac{1}{x}$-$\frac{1}{{x}^{2}}$=$\frac{(2x+1)(x-1)}{{x}^{2}}$,
由h′(x)>0可得x>1;由h′(x)<0可得0<x<1.
则h(x)的增区间为(1,+∞),减区间为(0,1);
(III)由题意可得f(x)≥g(x)对任意x∈[1,e]均成立,
即为x+$\frac{a}{x}$≥x-lnx,
即有a≥-xlnx,
令y=-xlnx,x∈[1,e],
则y′=-(1+lnx)<0,
即有y=-xlnx在[1,e]递减,
则y=-xlnx的最大值为0,
则a≥0,由a∈R且a≠0.
即有a>0.
则a的取值范围是(0,+∞).
点评 本题考查导数的运用:求切线方程和单调区间,同时考查不等式恒成立问题,注意运用参数分离,函数的单调性,属于中档题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
13.设i是虚数单位,在复平面内,复数z=2i(1+i)所对应的点落在( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
3.对于函数y=f(x),当x∈(0,+∞)时,总有f(x)<xf′(x),若m>n>0,则下列不等式中,恒成立的是( )
| A. | $\frac{f(m)}{n}$<$\frac{f(n)}{m}$ | B. | $\frac{f(m)}{m}$<$\frac{f(n)}{n}$ | C. | $\frac{f(m)}{n}$>$\frac{3f(n)}{m}$ | D. | $\frac{f(m)}{m}$>$\frac{f(n)}{n}$ |
10.设a,b∈R,则“a>b>1”是“a-b<a2-b2”的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充分必要条件 | D. | 既不充分也不必要条件 |
12.已知函数f(x)=cos(ωx+θ)为奇函数(0<θ<π),其图象与直线y=1的某两个交点的横坐标分别为x1、x2,且|x2-x1|的最小值为π,则( )
| A. | $ω=2,θ=\frac{π}{2}$ | B. | $ω=\frac{1}{2},θ=\frac{π}{2}$ | C. | $ω=\frac{1}{2},θ=\frac{π}{4}$ | D. | $ω=2,θ=\frac{π}{4}$ |
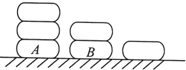 如图,桌面上摆有三串冰糖葫芦,第一串3课,第二串2颗,第三串1颗.小明每次从中取走一颗,若上面的冰糖葫芦取走后才能取下面的冰糖葫芦.则冰糖葫芦A恰好在第五次被取走,且冰糖葫芦B恰好在第六次被取走的取法数为12.
如图,桌面上摆有三串冰糖葫芦,第一串3课,第二串2颗,第三串1颗.小明每次从中取走一颗,若上面的冰糖葫芦取走后才能取下面的冰糖葫芦.则冰糖葫芦A恰好在第五次被取走,且冰糖葫芦B恰好在第六次被取走的取法数为12.