题目内容
4.(1)化简:$\frac{{cos({α-\frac{π}{2}})}}{{sin({\frac{5π}{2}+α})}}$•sin(α-2π)•cos(π-α);(2)计算:sin420°•cos750°+sin(-330°)•cos(-660°).
分析 (1)原式利用诱导公式化简,约分即可得到结果;
(2)原式利用诱导公式化简,再利用两角和与差的正弦函数公式及特殊角的三角函数值计算即可得到结果.
解答 解:(1)原式=$\frac{sinα}{cosα}$•sinα•(-cosα)=-sin2α;
(2)原式=sin60°cos30°+sin30°cos60°=sin(60°+30°)=sin90°=1.
点评 此题考查了运用诱导公式化简求值,熟练掌握诱导公式是解本题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
10.设a,b∈R,则“a>b>1”是“a-b<a2-b2”的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充分必要条件 | D. | 既不充分也不必要条件 |
12.已知函数f(x)=cos(ωx+θ)为奇函数(0<θ<π),其图象与直线y=1的某两个交点的横坐标分别为x1、x2,且|x2-x1|的最小值为π,则( )
| A. | $ω=2,θ=\frac{π}{2}$ | B. | $ω=\frac{1}{2},θ=\frac{π}{2}$ | C. | $ω=\frac{1}{2},θ=\frac{π}{4}$ | D. | $ω=2,θ=\frac{π}{4}$ |
9.设定义在R上的奇函数f(x)在区间(0,+∞)上单调递增,则不等式f(x-1)<0的解集是( )
| A. | (-∞,1) | B. | (1,+∞) | C. | (0,+∞) | D. | (-∞,0) |
14.△ABC中,若b=$\sqrt{3}$,c=1,∠A=30°,则a=( )
| A. | 1 | B. | $\sqrt{3}$ | C. | 2 | D. | $\sqrt{7}$ |
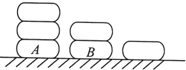 如图,桌面上摆有三串冰糖葫芦,第一串3课,第二串2颗,第三串1颗.小明每次从中取走一颗,若上面的冰糖葫芦取走后才能取下面的冰糖葫芦.则冰糖葫芦A恰好在第五次被取走,且冰糖葫芦B恰好在第六次被取走的取法数为12.
如图,桌面上摆有三串冰糖葫芦,第一串3课,第二串2颗,第三串1颗.小明每次从中取走一颗,若上面的冰糖葫芦取走后才能取下面的冰糖葫芦.则冰糖葫芦A恰好在第五次被取走,且冰糖葫芦B恰好在第六次被取走的取法数为12.