题目内容
14.已知集合A={-1,1,3},B={x|x<3},则A∩B={-1,1}.分析 由A与B,求出两集合的交集即可.
解答 解:∵A={-1,1,3},B={x|x<3},
∴A∩B={-1,1},
故答案为:{-1,1}
点评 此题考查了交集及其运算,熟练掌握交集的定义是解本题的关键.

练习册系列答案
 小博士期末闯关100分系列答案
小博士期末闯关100分系列答案 名校名师培优作业本加核心试卷系列答案
名校名师培优作业本加核心试卷系列答案
相关题目
5.在约束条件$\left\{\begin{array}{l}{x+2y≤4}\\{x-y≤1}\\{x+2≥0}\end{array}\right.$下,函数z=3x-y的最小值是( )
| A. | 9 | B. | 5 | C. | -5 | D. | -9 |
3.对于函数y=f(x),当x∈(0,+∞)时,总有f(x)<xf′(x),若m>n>0,则下列不等式中,恒成立的是( )
| A. | $\frac{f(m)}{n}$<$\frac{f(n)}{m}$ | B. | $\frac{f(m)}{m}$<$\frac{f(n)}{n}$ | C. | $\frac{f(m)}{n}$>$\frac{3f(n)}{m}$ | D. | $\frac{f(m)}{m}$>$\frac{f(n)}{n}$ |
9.设定义在R上的奇函数f(x)在区间(0,+∞)上单调递增,则不等式f(x-1)<0的解集是( )
| A. | (-∞,1) | B. | (1,+∞) | C. | (0,+∞) | D. | (-∞,0) |
 如图,函数y=f(x)是可导函数,曲线y=f(x)过点(2,3),且在x=2处的切线l在y轴上的截距为2,令g(x)=xf(x),则曲线y=g(x)在x=2处的切线方程是4x-y-2=0.
如图,函数y=f(x)是可导函数,曲线y=f(x)过点(2,3),且在x=2处的切线l在y轴上的截距为2,令g(x)=xf(x),则曲线y=g(x)在x=2处的切线方程是4x-y-2=0.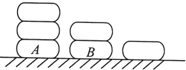 如图,桌面上摆有三串冰糖葫芦,第一串3课,第二串2颗,第三串1颗.小明每次从中取走一颗,若上面的冰糖葫芦取走后才能取下面的冰糖葫芦.则冰糖葫芦A恰好在第五次被取走,且冰糖葫芦B恰好在第六次被取走的取法数为12.
如图,桌面上摆有三串冰糖葫芦,第一串3课,第二串2颗,第三串1颗.小明每次从中取走一颗,若上面的冰糖葫芦取走后才能取下面的冰糖葫芦.则冰糖葫芦A恰好在第五次被取走,且冰糖葫芦B恰好在第六次被取走的取法数为12.