题目内容
1.已知数列{an}的前n项和Sn=2n+2-4.(1)求数列{an}的通项公式;
(2)设等差数列{bn}满足b7=a3,b15=a4,求数列{bn}的前n项和Tn.
分析 (1)求解n=1时,得出a1,n≥2时,运用an=Sn-Sn-1,合并通项公式即可.
(2)所以 根据条件得出方程组$\left\{\begin{array}{l}{{b}_{1}+6d=16}\\{{b}_{1}+14d=32}\end{array}\right.$,运用求和公式求解即可.
解答 (1)因为数列{an}的前N项和Sn=2n+2-4.
所以a1=S1=23-4=4
当n>1时,an=Sn-Sn-1=(2n+2-4)-(2n+1-4)=2n+1,
因为n=1时也适合,所以an=2n+1(n∈N*);
(2)设等差数列{bn}的首项为b1,公差为d,因为b7=a3,b15=a4,an=2n+1
所以 $\left\{\begin{array}{l}{{b}_{1}+6d=16}\\{{b}_{1}+14d=32}\end{array}\right.$,
解得$\left\{\begin{array}{l}{{b}_{1}=4}\\{d=2}\end{array}\right.$,
所以数列{bn}前n项和Tn=nb1$+\frac{n(n-1)}{2}$d=n2+3n.
点评 本题考察了数列的递推关系式的运用求解通项公式,关键是n=1别忘了,运用条件的方程组,计算能力.

练习册系列答案
相关题目
13.设i是虚数单位,在复平面内,复数z=2i(1+i)所对应的点落在( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
10.设a,b∈R,则“a>b>1”是“a-b<a2-b2”的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充分必要条件 | D. | 既不充分也不必要条件 |
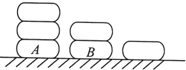 如图,桌面上摆有三串冰糖葫芦,第一串3课,第二串2颗,第三串1颗.小明每次从中取走一颗,若上面的冰糖葫芦取走后才能取下面的冰糖葫芦.则冰糖葫芦A恰好在第五次被取走,且冰糖葫芦B恰好在第六次被取走的取法数为12.
如图,桌面上摆有三串冰糖葫芦,第一串3课,第二串2颗,第三串1颗.小明每次从中取走一颗,若上面的冰糖葫芦取走后才能取下面的冰糖葫芦.则冰糖葫芦A恰好在第五次被取走,且冰糖葫芦B恰好在第六次被取走的取法数为12.