题目内容
19.已知△ABC中,cosA=$\frac{2\sqrt{5}}{5}$,cosB=$\frac{3\sqrt{10}}{10}$,则内角C等于( )| A. | $\frac{3π}{4}$ | B. | $\frac{2π}{3}$ | C. | $\frac{π}{2}$ | D. | $\frac{π}{4}$ |
分析 利用同角三角函数间的关系式可求得sinA=$\sqrt{1-co{s}^{2}A}$,sinB=$\sqrt{1-co{s}^{2}B}$,利用诱导公式与两角和的余弦函数公式即可求得cosC的值,结合C的范围即可得解.
解答 解:△ABC中,∵cosA=$\frac{2\sqrt{5}}{5}$>0,cosB=$\frac{3\sqrt{10}}{10}$>0,
∴A、B均为锐角,
∴sinA=$\sqrt{1-co{s}^{2}A}$=$\frac{\sqrt{5}}{5}$,同理可得sinB=$\sqrt{1-co{s}^{2}B}$=$\frac{\sqrt{10}}{10}$,
∴cosC=cos[π-(A+B)]=-cos(A+B)=-cosAcosB+sinAsinB=-$\frac{2\sqrt{5}}{5}$×$\frac{3\sqrt{10}}{10}$+$\frac{\sqrt{5}}{5}$×$\frac{\sqrt{10}}{10}$=-$\frac{\sqrt{2}}{2}$,
∵0<C<π,
∴可得:C=$\frac{3π}{4}$.
故选:A.
点评 本题考查同角三角函数间的关系式,考查诱导公式与两角和的余弦函数公式的应用,考查运算能力,属于中档题.

练习册系列答案
相关题目
 如图为函数f(x)=Asin(ωx+φ)(其中A>0,ω>0,|φ|<$\frac{π}{2}$)的一段图象.
如图为函数f(x)=Asin(ωx+φ)(其中A>0,ω>0,|φ|<$\frac{π}{2}$)的一段图象.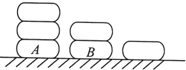 如图,桌面上摆有三串冰糖葫芦,第一串3课,第二串2颗,第三串1颗.小明每次从中取走一颗,若上面的冰糖葫芦取走后才能取下面的冰糖葫芦.则冰糖葫芦A恰好在第五次被取走,且冰糖葫芦B恰好在第六次被取走的取法数为12.
如图,桌面上摆有三串冰糖葫芦,第一串3课,第二串2颗,第三串1颗.小明每次从中取走一颗,若上面的冰糖葫芦取走后才能取下面的冰糖葫芦.则冰糖葫芦A恰好在第五次被取走,且冰糖葫芦B恰好在第六次被取走的取法数为12.