题目内容
7．已知函数f（x）=-x2-2x，g（x）=$\left\{\begin{array}{l}{x+1\\；x≤0}\\{x+\frac{1}{4x}\\；x＞0}\end{array}\right.$，若函数y=g[f（x）]-a有4个零点，则实数a的取值范围是[1，$\frac{5}{4}$）．分析 由题意可得函数y=g[f（x）]与函数y=a有4个交点，结合图象可得实数a的取值范围
解答 解：由题意可得函数y=g[f（x）]与函数y=a有4个交点，如图所示：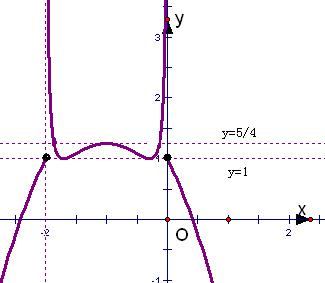
，
结合图象可得 1≤a＜$\frac{5}{4}$，
故答案为[1，$\frac{5}{4}$）．
点评 本题考查了根的存在性及根的个数判断，以及函数与方程的思想，解答关键是运用数形结合的思想，属于中档题．
练习册系列答案
相关题目
的定义域为（ ）
B．
D．
中，
，
，则
的值是（ ）
12．已知$\overrightarrow{a}$=（x，y），$\overrightarrow{b}$=（cosα，sinα），其中x，y，α∈R，若|$\overrightarrow{a}$|=9|$\overrightarrow{b}$|且$\overrightarrow{a}•\overrightarrow{b}$≤λ2+1恒成立，则实数λ的取值范围是（ ）
| A． | -2$\sqrt{2}$≤λ≤2$\sqrt{2}$ | B． | λ≤-2$\sqrt{2}$或λ≥2$\sqrt{2}$ | C． | λ≥2$\sqrt{2}$ | D． | λ≤-2$\sqrt{2}$ |
16．已知某校的体育场东侧有4个门，西侧有4个门，某同学要去体育场晨练，则他进出门的方案有（ ）
| A． | 16种 | B． | 8种 | C． | 32种 | D． | 64种 |
17．椭圆$\frac{x^2}{5}+\frac{y^2}{9}=1$的焦距是（ ）
| A． | 4 | B． | $\sqrt{14}$ | C． | 8 | D． | $2\sqrt{14}$ |