题目内容
19.已知f(x)=sin(ωx+$\frac{π}{6}$)的图象关于直线x=$\frac{π}{6}$对称,则ω的值是6k+2,k∈Z,.分析 由已知中f(x)=sin(ωx+$\frac{π}{6}$)的图象关于直线x=$\frac{π}{6}$对称,故当x=$\frac{π}{6}$时,f(x)取最大值,或最小值,(ω+1)$\frac{π}{6}$=kπ+$\frac{π}{2}$,k∈Z,进而得到答案.
解答 解:∵f(x)=sin(ωx+$\frac{π}{6}$)的图象关于直线x=$\frac{π}{6}$对称,
故当x=$\frac{π}{6}$时,f(x)取最大值,或最小值,
即(ω+1)$\frac{π}{6}$=kπ+$\frac{π}{2}$,k∈Z,
即ω=6k+2,k∈Z,
故答案为:6k+2,k∈Z,
点评 本题考查的知识点是正弦型函数的图象和性质,熟练掌握正弦型函数的图象和性质,是解答的关键.

练习册系列答案
 举一反三同步巧讲精练系列答案
举一反三同步巧讲精练系列答案 口算与应用题卡系列答案
口算与应用题卡系列答案 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案
相关题目
8.与直线y=$\frac{1}{2}$x+3平行且过点(0,-1)的直线方程为( )
| A. | 2x+y+1=0 | B. | x+2y+2=0 | C. | x-2y-2=0 | D. | 2x-y-1=0 |
 的等边三角形
的等边三角形 的中线
的中线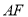 与中位线
与中位线 交于点
交于点 ,已知
,已知 是
是 绕
绕 旋转过程中的一个图形,则下列命题中正确的是( )
旋转过程中的一个图形,则下列命题中正确的是( )
 ;②
;② 平面
平面 ;③三棱锥
;③三棱锥 的体积有最大值.
的体积有最大值.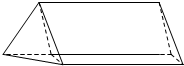 如图所示,放置在水平上的组合体由直三棱柱ABC-A1B1C1与正三棱柱B-ABCD组成(D在B1B的延长线上),它的正视图,俯视图,侧视图的面积分别为$2\sqrt{2}+1,2\sqrt{2}+1,1$.
如图所示,放置在水平上的组合体由直三棱柱ABC-A1B1C1与正三棱柱B-ABCD组成(D在B1B的延长线上),它的正视图,俯视图,侧视图的面积分别为$2\sqrt{2}+1,2\sqrt{2}+1,1$.