题目内容
12.已知$\overrightarrow{a}$=(x,y),$\overrightarrow{b}$=(cosα,sinα),其中x,y,α∈R,若|$\overrightarrow{a}$|=9|$\overrightarrow{b}$|且$\overrightarrow{a}•\overrightarrow{b}$≤λ2+1恒成立,则实数λ的取值范围是( )| A. | -2$\sqrt{2}$≤λ≤2$\sqrt{2}$ | B. | λ≤-2$\sqrt{2}$或λ≥2$\sqrt{2}$ | C. | λ≥2$\sqrt{2}$ | D. | λ≤-2$\sqrt{2}$ |
分析 由已知中$\overrightarrow{b}$=(cosα,sinα),我们可以得到|$\overrightarrow{b}$|=1,再由|$\overrightarrow{a}$|=9|$\overrightarrow{b}$|可设$\overrightarrow{a}$=9(sinα,cosα),代入平面向量数量积的坐标运算公式,求出$\overrightarrow{a}$•$\overrightarrow{b}$的取值范围,结合函数恒成立的条件,可以得到一个关于λ的不等式,解不等式即可得到实数λ的取值范围.
解答 解:∵$\overrightarrow{b}$=(cosα,sinα),|$\overrightarrow{a}$|=9|$\overrightarrow{b}$|,
∴设$\overrightarrow{a}$=9(sinθ,cosθ)
则$\overrightarrow{a}$•$\overrightarrow{b}$=9sinθ•cosα+9cosθ•sinα=9sin(α+θ)∈[-9,9]
若$\overrightarrow{a}$•$\overrightarrow{b}$≤λ2+1恒成立,
则λ2≥8,
解得λ≥2$\sqrt{2}$或λ≤-2$\sqrt{2}$,
故选:B.
点评 本题考查的知识点是平面向量数量积的运算,函数恒成立问题,其中利用函数恒成立的条件,结合已知条件,得到一个关于λ的不等式,是解答本题的关键.

练习册系列答案
 浙江之星学业水平测试系列答案
浙江之星学业水平测试系列答案 高效智能课时作业系列答案
高效智能课时作业系列答案
相关题目
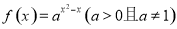 .
. ,求
,求 的单调递增区间;
的单调递增区间; ,求使
,求使 成立的
成立的 的集合.
的集合. 如图,四边形ABCD是梯形,四边形CDEF是矩形,且平面ABCD⊥平面CDEF,∠BAD=∠CDA=90°,AB=AD=DE=CD=2,M是线段AE上的动点.
如图,四边形ABCD是梯形,四边形CDEF是矩形,且平面ABCD⊥平面CDEF,∠BAD=∠CDA=90°,AB=AD=DE=CD=2,M是线段AE上的动点.