题目内容
15.已知f(x)=|2x-1|-ax-3(a是常数,a∈R)恰有两个不同的零点,则a的取值范围为(-2,2).分析 f(x)=|2x-1|-ax-3恰有两个不同的零点可化为函数y=|2x-1|与函数y=ax+3有两个不同的交点;作图求解即可.
解答 解:f(x)=|2x-1|-ax-3恰有两个不同的零点可化为:
函数y=|2x-1|与函数y=ax+3有两个不同的交点;
作函数y=|2x-1|与函数y=ax+3的图象,如图示: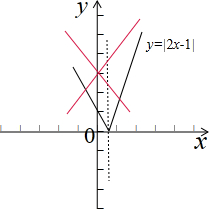 ,
,
由图象可知,
当-2<a<2时,数y=|2x-1|与函数y=ax+3的图象有两个不同的交点,
即f(x)=|2x-1|-ax-3恰有两个不同的零点;
故答案为:(-2,2).
点评 本题考是了函数的零点与函数的图象的应用,同时考查了数形结合的思想应用,属于基础题.

练习册系列答案
相关题目
5.△ABC中,三个角A,B,C所对的边a,b,c满足a2+b2=c2-$\sqrt{3}$ab,则C=( )
| A. | 150° | B. | 135° | C. | 120° | D. | 60° |
 满足
满足 ,则称数列
,则称数列 为调和数列,且
为调和数列,且 ,则
,则 .
.