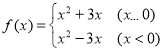题目内容
【题目】已知从1开始的连续奇数蛇形排列形成宝塔形数表,第一行为1,第二行为3,5,第三行为7,9,11,第四行为13,15,17,19,…,如图所示,在宝塔形数表中位于第![]() 行、第
行、第![]() 列的数记为
列的数记为![]() ,比如
,比如![]() ,
,![]() ,
,![]() .若
.若![]() ,则
,则![]() ______.
______.
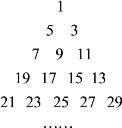
【答案】65
【解析】
奇数数列bn=2n﹣1=2019,从而2019为第1010个奇数.每行的项数记为cm,则cm=m,其前i项和为![]() 个奇数,则第1行到第44行末共有990个奇数,第1行到第45行末共有1035个奇数,从而2019位于第45行,从右到左第20个,由此能求出i+j.
个奇数,则第1行到第44行末共有990个奇数,第1行到第45行末共有1035个奇数,从而2019位于第45行,从右到左第20个,由此能求出i+j.
解:∵将正奇数按如图所示的规律排列,在数表中位于第i行,第j列的数记为ai,j,ai,j=2019,∴奇数数列bn=2n﹣1=2019,解得n=1010,即2019为第1010个奇数.
每行的项数记为cm,则cm=m,其前i项和为:1+2+3+…+i![]() 个奇数,
个奇数,
则第1行到第44行末共有990个奇数,
第1行到第45行末共有1035个奇数,
则2019位于第45行,而第45行是从左到右依次递增,且共有45个奇数,
∴2019位于第45行,从左到右第20个,
∴i=45,j=20,∴i+j=45+20=65.

【题目】在甲、乙两个班级进行数学考试,按照大于等于120分为优秀,120分以下为非优秀统计成绩后,得到如下的2×2列联表.已知在全部105人中抽到随机抽取1人为优秀的概率为![]() .
.
优秀 | 非优秀 | 总计 | |
甲班 | 10 | ||
乙班 | 30 | ||
合计 |
(1)请完成上面的列联表;
(2)根据列联表的数据,若按95%的可能性要求,能否认为“成绩与班级有关系”?
P(K2≥x0) | 0.50 | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
x0 | 0.455 | 0.708 | 1.323 | 2.072 | 2.076 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
参考公式及数据:K2=![]() .
.