题目内容
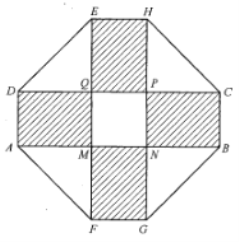
【题目】某小区要建一个八边形的休闲区，如图所示，它的主要造型平面图是由两个相同的矩形
和
构成的面积为
的十字形区域.计划在正方形
上建一个花坛，造价为4200元/
，在四个相同的矩形（图中阴影部分）上铺设花岗岩地面，造价为210元/，再在四个等腰直角三角形上铺设草坪，造价为80元/.求当
的长度为多少时，建设这个休闲区的总价最低.
【答案】当
的长度为
时，建设休闲区总价最低
【解析】
由题意，十字形区域面积固定，造型随着的改变而改变，从而使得总费用也随之变化. 设的长度为
米，建设休闲区的总价为y元.计算出中间正方形区域面积、四个矩形面积之和、四块等腰直角三角形的面积之和，即可求出总价y关于的函数解析式，再利用基本不等式求最小值，即可求出的值.
设的长度为
，建设休闲区的总价为y元，
则中间正方形区域面积为
，四个矩形面积之和为
，
，四块等腰直角三角形的面积之和为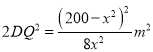
.
∴
.
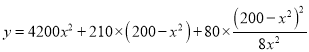
由
，
，可得
.
，
当且仅当
，即
时，等号成立.
所以，当的长度为时，建设休闲区总价最低.
练习册系列答案
天天练口算系列答案
相关题目
