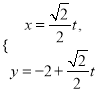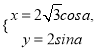题目内容
【题目】已知抛物线![]() (
(![]() ),直线
),直线![]() 与抛物线
与抛物线![]() 交于
交于![]() (点
(点![]() 在点
在点![]() 的左侧)两点,且
的左侧)两点,且![]() .
.
(1)求抛物线![]() 在
在![]() 两点处的切线方程;
两点处的切线方程;
(2)若直线![]() 与抛物线
与抛物线![]() 交于
交于![]() 两点,且
两点,且![]() 的中点在线段
的中点在线段![]() 上,
上, ![]() 的垂直平分线交
的垂直平分线交![]() 轴于点
轴于点![]() ,求
,求![]() 面积的最大值.
面积的最大值.
【答案】(1) ![]() (2)
(2) ![]()
【解析】试题分析:(1)第(1)问,先求出抛物线的方程![]() 得到
得到![]() ,再求导求出切线斜率,最后求出抛物线
,再求导求出切线斜率,最后求出抛物线![]() 在
在![]() 两点处的切线方程.(2)第(2)问,先利用弦长公式求出
两点处的切线方程.(2)第(2)问,先利用弦长公式求出![]() ,再利用点到直线的距离求三角形的高
,再利用点到直线的距离求三角形的高![]() ,最后写出面积的表达式
,最后写出面积的表达式![]() ,再换元利用导数求它的最大值.
,再换元利用导数求它的最大值.
试题解析:
(1)由![]() ,令
,令![]() ,得
,得![]() ,所以
,所以![]() ,解得
,解得![]() ,
, ![]() ,由
,由![]() ,得
,得![]() ,故
,故![]() 所以在
所以在![]() 点的切线方程为
点的切线方程为![]() ,即
,即![]() ,同理可得在
,同理可得在![]() 点的切线方程为
点的切线方程为![]() .
.
(2)由题意得直线![]() 的斜率存在且不为0,
的斜率存在且不为0,
故设![]() ,
, ![]() ,
, ![]() ,由
,由![]() 与
与![]() 联立,
联立,
得![]() ,
, ![]() ,
,
所以![]() ,
, ![]() ,
,
故![]() .
.
又![]() ,所以
,所以![]() ,所以
,所以![]() ,
,
由![]() ,得
,得![]() 且
且![]() .
.
因为![]() 的中点为
的中点为![]() ,所以
,所以![]() 的垂直平分线方程为
的垂直平分线方程为![]() ,令
,令![]() ,得
,得![]() ,即
,即![]() ,所以点
,所以点![]() 到直线
到直线![]() 的距离
的距离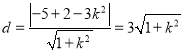 ,
,
所以![]()
![]() .
.
令![]() ,则
,则![]() ,则
,则![]() ,故
,故![]() .
.
设![]() ,则
,则![]() ,结合
,结合![]() ,令
,令![]() ,得
,得![]() ;
;
令![]() ,得
,得![]() ,所以当
,所以当![]() ,即
,即![]() 时,
时, ![]() .
.

练习册系列答案
 寒假创新型自主学习第三学期寒假衔接系列答案
寒假创新型自主学习第三学期寒假衔接系列答案
相关题目