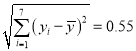题目内容
【题目】已知函数![]() ,
,![]() 为自然对数的底数.
为自然对数的底数.
(1)讨论![]() 的单调性;
的单调性;
(2)若函数![]() 的图象与直线
的图象与直线![]() 交于
交于![]() 两点,线段
两点,线段![]() 中点的横坐标为
中点的横坐标为![]() ,证明:
,证明: ![]() 为函数
为函数![]() 的导函数).
的导函数).
【答案】(1) 当![]() 时,
时,![]() 在
在![]() 上单调递减,在
上单调递减,在![]() 上单调递增,当
上单调递增,当![]() 时,
时,![]() 在
在![]() 上单调递增,当
上单调递增,当![]() 时,
时,![]() 在
在![]() 上单调递增,在
上单调递增,在![]() 上单调递减;(2)证明见解析.
上单调递减;(2)证明见解析.
【解析】
试题分析:(1)借助题设条件运用导数与函数的单调性的关系与分类整合思想求解;(2)依据题设构造函数运用导数知识推证.
试题解析:
(1)由题可知,![]() . ①当
. ①当![]() 时,
时,
令![]() ,则
,则![]() ,令
,令![]() ,则
,则![]() .
.
②当![]() 时,
时,![]() .③当
.③当![]() 时,令
时,令![]() ,则
,则![]() ,令
,令![]() ,则
,则![]() ,综上,①当
,综上,①当![]() 时,
时,![]() 在
在![]() 上单调递减,在
上单调递减,在![]() 上单调递增;②当
上单调递增;②当![]() 时,
时,![]() 在
在![]() 上单调递增;③当
上单调递增;③当![]() 时,
时,![]() 在
在![]() 上单调递增,在
上单调递增,在![]() 上单调递减.
上单调递减.
(2)
![]() ,
,![]() ,当
,当![]() 时,
时,
![]() 在
在![]() 上单调递增,与
上单调递增,与![]() 轴不可能有两个交点,故
轴不可能有两个交点,故![]() .
.
当![]() 时,令
时,令![]() ,则
,则![]() ;令
;令![]() ,则
,则![]() .
.
故![]() 在
在![]() 上单调递增,在
上单调递增,在![]() 上单调递减.不妨设
上单调递减.不妨设![]() ,
,
且![]() .要证
.要证![]() ,需证
,需证![]() ,
,
即证![]() ,
,
又![]() ,所以只需证
,所以只需证![]() .
.
即证:当![]() 时,
时,![]() .
.
设![]() ,
,
则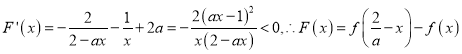 在
在![]() 上单调递减,
上单调递减,
又![]() ,故
,故![]() .
.

练习册系列答案
相关题目