题目内容

5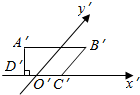．如图所示，A′B′C′D′是一个水平放置的平面图形的斜二测直观图，已知A′B′C′D′是一个直角梯形，A′B′∥C′D′，A′D′⊥C′D′，且B′C′与y轴平行，又A′B′=21，DC′′=9，A′D′=12，试求梯形A′B′C′D′的原图形ABCD的面积．

分析 由题意，梯形A′B′C′D′的原图形ABCD的高为24$\sqrt{2}$，AB=21，DC=9，即可求出原图形ABCD的面积．

解答 解：由题意，梯形A′B′C′D′的原图形ABCD的高为24$\sqrt{2}$，AB=21，DC=9，
∴原图形ABCD的面积S=$\frac{21+9}{2}×24\sqrt{2}$=360$\sqrt{2}$．

点评 本题考查斜二测画法，直观图与平面图形的面积的比例关系的应用，考查计算能力．

练习册系列答案
相关题目
15．已知函数f（x）=sin（ωx+φ）（0＜φ＜π，ω＞0）为偶函数，且函数y=f（x）图象的两相邻对称轴间的距离为$\frac{π}{2}$．
（1）求f（$\frac{π}{8}$）的值；
（2）函数h（x）=af（$\frac{x}{2}$）-sin2x有最小值为-1，求a的值．
16．已知函数y=$\frac{1+4x+{x}^{2}}{1+{x}^{2}}$，求函数的值域．
13．求函数y=$\frac{{x}^{2}-2x+3}{{x}^{2}-x+2}$的值域．
20．设函数f（x）=$\left\{\begin{array}{l}{3cosx\\;x＜0}\\{2x+b\\;x≥0}\end{array}\right.$，如果f（x）在x=0处连续，则b=（　　）
A．1B．2C．3D．4
10．数列{an}满足an+1=an+$\frac{8（n+1）}{（2n+1）^{2}（2n+3）^{2}}$，a1=$\frac{8}{9}$，求数列{an}的通项公式．
17．若函数f（x+1）的定义域为[-$\frac{1}{2}$，2]，求函数f（x-1）的定义域．
14．若C${\;}_{21}^{k-4}$＜C${\;}_{21}^{k-2}$＜C${\;}_{21}^{k-1}$（k∈N），则k的取值范围是（　　）
A．[5，11]B．[4，11]C．[4，12]D．[4，15]
15．化简：$\frac{1}{2！}$+$\frac{2}{3！}$+$\frac{3}{4！}$+…+$\frac{n-1}{n!}$．（n∈N*，n≥2）

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网