题目内容

20．设函数f（x）=$\left\{\begin{array}{l}{3cosx\\;x＜0}\\{2x+b\\;x≥0}\end{array}\right.$，如果f（x）在x=0处连续，则b=（　　）
A．1B．2C．3D．4

分析 根据函数连续性的概念，f（x）在x=0的左右两边相等，求出b的值．

解答 解：∵函数f（x）=$\left\{\begin{array}{l}{3cosx\\;x＜0}\\{2x+b\\;x≥0}\end{array}\right.$，
且f（x）在x=0处连续，
∴f（0）=b=3cos0，
∴b=3．
故选：C．

点评 本题考查了函数连续性的概念与应用问题，是基础题目．

练习册系列答案
相关题目
10．四个非零数字之和是8，这四个数字可以组成35个不同的四位数．
11．已知数列{an}为等差数列，且a1+a3=10，a7+a9=20，则a5=$\frac{15}{2}$．
8．求函数值域．
（1）f（x）=$\sqrt{1-x}$+$\sqrt{x+3}$；
（2）f（x）=$\sqrt{1-x}$-$\sqrt{x+3}$．
15．已知数列{an}中，a1=1，前n项和为Sn=$\frac{n+2}{3}$an．
（1）求数列{an}的通项公式；
（2）设bn=$\frac{1}{{n}^{2}+2{a}_{n}}$，数列{bn}的前n项和Tn，证明：Tn＜$\frac{2}{3}$；
（3）设cn=$\frac{2n+1}{{a}_{n}^{2}}$，问：是否存在常数M，使得对所有的n∈N*，都有c1+c2+…+cn＜M．若存在，求M的最小值，若不存在，说明理由．
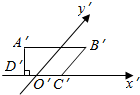5．如图所示，A′B′C′D′是一个水平放置的平面图形的斜二测直观图，已知A′B′C′D′是一个直角梯形，A′B′∥C′D′，A′D′⊥C′D′，且B′C′与y轴平行，又A′B′=21，DC′′=9，A′D′=12，试求梯形A′B′C′D′的原图形ABCD的面积．
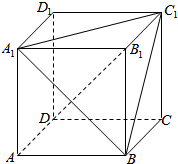12．如图，在正方体ABCD-A1B1C1D1中．
（1）求BC1与平面ABCD所成角的大小；
（2）求证：BC1⊥B1D；
（3）求证：B1D⊥平面A1BC1．
9．若y=$\frac{ax+b}{{x}^{2}+1}$的值域[-1，4]，求a，b的值．
10．对于定义在R上的函数f（x），有下述四个命题；
①若y=f（x）是奇函数，则y=f（x-1）的图象关于点A（1，0）对称；
②若函数y=f（x+1）与y=f（1-x）的图象关于直线x=1对称；
③如果函数y=f（x）满足f（x+1）=f（1-x），f（x+3）=f（3-x），那么该函数以4为周期．
其中正确命题的序号为①③．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网