题目内容
10.数列{an}满足an+1=an+$\frac{8(n+1)}{(2n+1)^{2}(2n+3)^{2}}$,a1=$\frac{8}{9}$,求数列{an}的通项公式.分析 由数列递推式得到an+1-an=$\frac{8(n+1)}{(2n+1)^{2}(2n+3)^{2}}$,然后利用裂项相消法求得数列{an}的通项公式.
解答 解:∵an+1=an+$\frac{8(n+1)}{(2n+1)^{2}(2n+3)^{2}}$,
∴an+1-an=$\frac{1}{(2n+1)^{2}}-\frac{1}{(2n+3)^{2}}$,
则当n≥2时,an=(an-an-1)+(an-1-an-2)+…+(a2-a1)
=$\frac{1}{(2n-1)^{2}}-\frac{1}{(2n+1)^{2}}+\frac{1}{(2n-3)^{2}}-\frac{1}{(2n-1)^{2}}+…+$$\frac{1}{{3}^{2}}-\frac{1}{{5}^{2}}$
=$\frac{1}{9}-\frac{1}{(2n+1)^{2}}=\frac{4{n}^{2}+4n-8}{9(2n+1)^{2}}$.
验证当n=1时,上式不成立.
∴${a}_{n}=\left\{\begin{array}{l}{\frac{8}{9},n=1}\\{\frac{4{n}^{2}+4n-8}{9(2n+1)^{2}},n≥2}\end{array}\right.$.
点评 本题考查数列递推式,训练了裂项相消法求数列的和,是中档题.

练习册系列答案
 海淀黄冈名师导航系列答案
海淀黄冈名师导航系列答案 普通高中同步练习册系列答案
普通高中同步练习册系列答案
相关题目
20.若$\sqrt{4{a}^{2}-4a+1}$=$\root{3}{(1-2a)^{3}}$,则实数a的取值范围是( )
| A. | a∈R | B. | a=$\frac{1}{2}$ | C. | a>$\frac{1}{2}$ | D. | a≤$\frac{1}{2}$ |
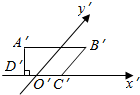 如图所示,A′B′C′D′是一个水平放置的平面图形的斜二测直观图,已知A′B′C′D′是一个直角梯形,A′B′∥C′D′,A′D′⊥C′D′,且B′C′与y轴平行,又A′B′=21,DC′′=9,A′D′=12,试求梯形A′B′C′D′的原图形ABCD的面积.
如图所示,A′B′C′D′是一个水平放置的平面图形的斜二测直观图,已知A′B′C′D′是一个直角梯形,A′B′∥C′D′,A′D′⊥C′D′,且B′C′与y轴平行,又A′B′=21,DC′′=9,A′D′=12,试求梯形A′B′C′D′的原图形ABCD的面积. 在一次青年歌手大奖赛中,七位评委为某参赛选手打出的分数的茎叶图如图所示,去掉一个最高分和一个最低分,所剩数据的平均值为83.
在一次青年歌手大奖赛中,七位评委为某参赛选手打出的分数的茎叶图如图所示,去掉一个最高分和一个最低分,所剩数据的平均值为83.