题目内容
15.已知函数f(x)=sin(ωx+φ)(0<φ<π,ω>0)为偶函数,且函数y=f(x)图象的两相邻对称轴间的距离为$\frac{π}{2}$.(1)求f($\frac{π}{8}$)的值;
(2)函数h(x)=af($\frac{x}{2}$)-sin2x有最小值为-1,求a的值.
分析 (1)由条件利用正弦函数、余弦函数的奇偶性,求得φ的值,再根据余弦函数的图象的对称性以及周期性求得ω的值,可得函数的解析式,从而求得f($\frac{π}{8}$)的值.
(2)由题意可得h(x)=cos2x+acosx-1有最小值为-1,而cosx∈[-1,1],再利用二次函数的性质、分类讨论求得a的值,综合可得结论.
解答 解:(1)由函数f(x)=sin(ωx+φ)(0<φ<π,ω>0)为偶函数,
可得φ=$\frac{π}{2}$,f(x)=cosωx.
再根据函数y=f(x)图象的两相邻对称轴间的距离为$\frac{1}{2}•\frac{2π}{ω}$=$\frac{π}{2}$,求得ω=2,
∴f(x)=cos2x,∴f($\frac{π}{8}$)=cos$\frac{π}{4}$=$\frac{\sqrt{2}}{2}$.
(2)函数h(x)=af($\frac{x}{2}$)-sin2x=acosx-(1-cos2x)=cos2x+acosx-1有最小值为-1,
而cosx∈[-1,1],
∴当-$\frac{a}{2}$<-1,即a>2时,h(x)的最小值为1-a-1=-1,求得a=1(舍去).
当-$\frac{a}{2}$∈[-1,1],即-2≤a≤2时,h(x)的最小值为$\frac{-4{-a}^{2}}{4}$=-1,求得a=0.
当-$\frac{a}{2}$>1,即a<-2时,h(x)的最小值为 1+a-1=-1,求得a=-1(舍去).
综上可得,a=0.
点评 本题主要考查正弦函数、余弦函数的奇偶性,余弦函数的图象的对称性以及周期性,二次函数的性质应用,体现了转化、分类讨论的数学思想,属于中档题.

练习册系列答案
 赢在课堂名师课时计划系列答案
赢在课堂名师课时计划系列答案 天天向上课时同步训练系列答案
天天向上课时同步训练系列答案
相关题目
3.5个人排队,其中甲、乙、丙3人按甲、乙、丙的顺序排队的方法有( )
| A. | 12 | B. | 20 | C. | 16 | D. | 120 |
4.已知$\overrightarrow{m}$=(sin(2α+β),cosβ),$\overrightarrow{n}$=(cos(2α-β),sinβ),且$\overrightarrow{m}$∥$\overrightarrow{n}$,则锐角α,β的值为( )
| A. | α=$\frac{π}{4}$,β任意 | B. | α任意,β=$\frac{π}{4}$ | C. | α=β=$\frac{π}{4}$ | D. | α任意,β任意 |
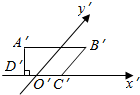 如图所示,A′B′C′D′是一个水平放置的平面图形的斜二测直观图,已知A′B′C′D′是一个直角梯形,A′B′∥C′D′,A′D′⊥C′D′,且B′C′与y轴平行,又A′B′=21,DC′′=9,A′D′=12,试求梯形A′B′C′D′的原图形ABCD的面积.
如图所示,A′B′C′D′是一个水平放置的平面图形的斜二测直观图,已知A′B′C′D′是一个直角梯形,A′B′∥C′D′,A′D′⊥C′D′,且B′C′与y轴平行,又A′B′=21,DC′′=9,A′D′=12,试求梯形A′B′C′D′的原图形ABCD的面积.