题目内容
16.已知函数y=$\frac{1+4x+{x}^{2}}{1+{x}^{2}}$,求函数的值域.分析 原函数可变成$y=1+\frac{4x}{1+{x}^{2}}$,可讨论x=0,x>0,x<0三种情况:x=0时可得到y=0,而对于x>0,和x<0的情况,可将原函数变成$y=1+\frac{4}{x+\frac{1}{x}}$,这样根据基本不等式即可得出y的范围,合并三种情况得到的y的范围,从而得出原函数的值域.
解答 解:$y=\frac{1+{x}^{2}+4x}{1+{x}^{2}}=1+\frac{4x}{1+{x}^{2}}$;
①若x=0,则y=1;
②若x>0,则$y=1+\frac{4}{x+\frac{1}{x}}$;
$x+\frac{1}{x}≥2$,x=1时取“=”;
∴$0<\frac{1}{x+\frac{1}{x}}≤\frac{1}{2}$;
∴1<y≤3;
③若x<0,y=$1+\frac{4}{x+\frac{1}{x}}$;
$x+\frac{1}{x}=-[(-x)+\frac{1}{-x}]≤-2$;
∴$-\frac{1}{2}≤\frac{1}{x+\frac{1}{x}}<0$;
∴-1≤y<1;
∴综上得原函数的值域为:[-1,3].
点评 考查函数值域的概念,分离常数法的运用,利用基本不等式求函数值域的方法.

练习册系列答案
相关题目
4.已知$\overrightarrow{m}$=(sin(2α+β),cosβ),$\overrightarrow{n}$=(cos(2α-β),sinβ),且$\overrightarrow{m}$∥$\overrightarrow{n}$,则锐角α,β的值为( )
| A. | α=$\frac{π}{4}$,β任意 | B. | α任意,β=$\frac{π}{4}$ | C. | α=β=$\frac{π}{4}$ | D. | α任意,β任意 |
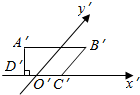 如图所示,A′B′C′D′是一个水平放置的平面图形的斜二测直观图,已知A′B′C′D′是一个直角梯形,A′B′∥C′D′,A′D′⊥C′D′,且B′C′与y轴平行,又A′B′=21,DC′′=9,A′D′=12,试求梯形A′B′C′D′的原图形ABCD的面积.
如图所示,A′B′C′D′是一个水平放置的平面图形的斜二测直观图,已知A′B′C′D′是一个直角梯形,A′B′∥C′D′,A′D′⊥C′D′,且B′C′与y轴平行,又A′B′=21,DC′′=9,A′D′=12,试求梯形A′B′C′D′的原图形ABCD的面积.