Question

8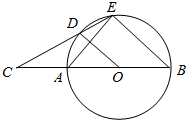．如图，AB是⊙O的直径，延长BA至C，使BC=3AC，过点C作⊙O的割线交⊙O于D、E两点，且∠ADC=∠AOD．
（1）证明：AD=DE；
（2）若AD=2，求四边形BEDO的面积．

Answer 1

分析 （1）证明OD∥BE，利用BE⊥AE，可得OD⊥AE，D是$\widehat{AE}$的中点，即可证明AD=DE；
（2）若AD=2，设AE的中点为F，求出OF=$\frac{3}{2}$$\sqrt{2}$，BE=3$\sqrt{2}$，EF=$\frac{\sqrt{14}}{2}$，利用梯形的面积公式，即可求四边形BEDO的面积．

解答 （1）证明：∵A，D，E，B四点共圆，
∴∠ADC=∠B
∵∠ADC=∠AOD，
∴∠B=∠AOD，
∴OD∥BE，
∵AB是⊙O的直径，
∴∠AEB=90°，
∴BE⊥AE，
∴OD⊥AE，
∴D是$\widehat{AE}$的中点，
∴AD=DE；
（2）解：由（1）知道，△CDA∽△COD，
∴$\frac{CD}{CO}=\frac{DA}{OD}$，
∵BC=3AC，
∴CD=2DA，
∵AD=2，
∴CD=4，
由割线定理可得4×6=CA×3CA，
∴CA=2$\sqrt{2}$，
设AE的中点为F，则$\frac{1}{2}$×$2\sqrt{2}$×AF=$\frac{1}{2}×2×\sqrt{8-1}$，
∴AF=$\frac{\sqrt{14}}{2}$，
∴OF=$\frac{3}{2}$$\sqrt{2}$，BE=3$\sqrt{2}$，EF=$\frac{\sqrt{14}}{2}$，
∴四边形BEDO的面积S=$\frac{1}{2}$（$\frac{3}{2}$$\sqrt{2}$+3$\sqrt{2}$）×$\frac{\sqrt{14}}{2}$=$\frac{9\sqrt{7}}{4}$．

点评 本题考查四点共圆的性质，考查割线定理，考查四边形BEDO的面积，考查学生分析解决问题的能力，属于中档题．