题目内容
13.已知函数y=Asin(ωx+φ)(A>0,0<φ<$\frac{π}{2}$)的图象上一个最低点是(-6,-$\sqrt{2}$),由这个最低点到相邻的最高点的曲线与x轴的交点是(-2,0),求函数解析式.分析 根据函数的最低点求出A,根据最低点和x轴的交点得函数的周期T,利用周期公式T=$\frac{2π}{ω}$可求ω,然后求φ即可.
解答 解:∵f(x)的图象上一个最低点是(-6,-$\sqrt{2}$),
∴A=$\sqrt{2}$,
∵这个最低点到相邻的最高点的曲线与x轴的交点是(-2,0),
∴$\frac{T}{4}$=-2-(-6)=6-2=4,
∴T=16,由周期公式 $T=\frac{2π}{ω}$=16,可得ω=$\frac{π}{8}$,
则y=$\sqrt{2}$sin($\frac{π}{8}$x+φ),
由函数图象过(-6,-$\sqrt{2}$),
代入可得$\sqrt{2}$sin($-\frac{6π}{8}$+φ)=$-\sqrt{2}$,
即sin($-\frac{3π}{4}$+φ)=-1,
即$-\frac{3π}{4}$+φ=2kπ-$\frac{π}{2}$,即φ=$\frac{π}{4}$+2kπ,
∵0<φ<$\frac{π}{2}$,
∴当k=0时,φ=$\frac{π}{4}$,
即f(x)=$\sqrt{2}$sin($\frac{π}{8}$x+$\frac{π}{4}$).
点评 本题主要考查了利用正弦函数的性质求解函数y=Asin(ωx+φ)的解析式,其步骤:由函数的最值求解A;由函数的周期求解ω;再把函数所过的一点(一般用最值点)代入可求φ,从而可求函数的解析式.

练习册系列答案
 走进文言文系列答案
走进文言文系列答案
相关题目
4.设△ABC的内角A,B,C所对应的边分别是a,b,c,若A=60°,a=$\sqrt{13}$,b=4,则c=( )
| A. | 1 | B. | 3 | C. | 1或3 | D. | 无解 |
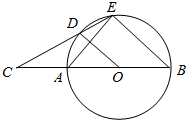 如图,AB是⊙O的直径,延长BA至C,使BC=3AC,过点C作⊙O的割线交⊙O于D、E两点,且∠ADC=∠AOD.
如图,AB是⊙O的直径,延长BA至C,使BC=3AC,过点C作⊙O的割线交⊙O于D、E两点,且∠ADC=∠AOD.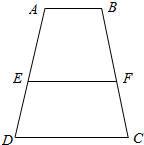 在梯形ABCD中,AB=a,CD=b,a<b,EF为一线段,若S四边形ABFE=S四边形CDEF,且∠BFE=∠D,求EF的长(用a,b表示).
在梯形ABCD中,AB=a,CD=b,a<b,EF为一线段,若S四边形ABFE=S四边形CDEF,且∠BFE=∠D,求EF的长(用a,b表示).