题目内容
18.已知a1=1,an+1=pan-n-1(p∈R,n∈N*)(1)当p=1时,求数列{an}的通项公式;
(2)设bn=an-n-2,若数列{bn}为等比数列,求p的值.
分析 (1)当p=1时,得到an+1-an=n-1,利用累加法即可求数列{an}的通项公式;
(2)设bn=an-n-2,根据数列的递推关系,结合等比数列的定义即可得到结论.
解答 解:(1)当p=1时,an+1=an-n-1,
即an+1-an=n-1,
则a2-a1=0,
a3-a2=1,
a4-a3=2,
…
an-an-1=n-2,
等式两边同时相加得
an-a1=0+1+2+…+(n-2)=$\frac{(n-1)(0+n-2)}{2}$=$\frac{{n}^{2}-3n+2}{2}$,
∴an=$\frac{{n}^{2}-3n+2}{2}$+1=$\frac{{n}^{2}-3n+4}{2}$;
(2)∵an+1=pan-n-1,
∴an+1-(n+1)-2=pan-n-1-(n+1)-2=pan-2n-4=2($\frac{p}{2}$an-n-2),
若数列{bn}为等比数列,则$\frac{p}{2}$=1,即p=2.
点评 本题主要考查递推数列的应用,利用列举法求数列的通项公式,以及结合等比数列的定义和性质是解决本题的关键.

练习册系列答案
相关题目
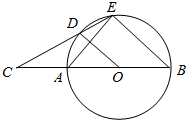 如图,AB是⊙O的直径,延长BA至C,使BC=3AC,过点C作⊙O的割线交⊙O于D、E两点,且∠ADC=∠AOD.
如图,AB是⊙O的直径,延长BA至C,使BC=3AC,过点C作⊙O的割线交⊙O于D、E两点,且∠ADC=∠AOD.