题目内容
19.已知函数f(x)=$\left\{\begin{array}{l}{f(x+3),x<6}\\{lo{g}_{a}x,x≥6}\end{array}\right.$,若f(-1)<3,则a的取值范围是( )| A. | (0,1)∪(2,+∞) | B. | (2,+∞) | C. | (0,1) | D. | (1,2) |
分析 根据已知中函数的解析式,可得f(-1)=loga8,结合f(-1)<3和对数函数的图象和性质,换底公式的推论,可得满足条件的a的取值范围.
解答 解:∵数f(x)=$\left\{\begin{array}{l}{f(x+3),x<6}\\{lo{g}_{a}x,x≥6}\end{array}\right.$,
则f(-1)=f(2)=f(5)=f(8)=loga8,
若f(-1)<3,则loga8<3,
若a∈(0,1),则loga8<0<3,满足条件;
若a∈(1,+∞),则loga8>0,loga8<3可化为$lo{g}_{8}a>\frac{1}{3}$,解得a>2.
综上a的取值范围是(0,1)∪(2,+∞),
故选:A
点评 本题考查的知识点是分段函数的应用,函数求值,难度不大,属于中档题.

练习册系列答案
相关题目
4.设△ABC的内角A,B,C所对应的边分别是a,b,c,若A=60°,a=$\sqrt{13}$,b=4,则c=( )
| A. | 1 | B. | 3 | C. | 1或3 | D. | 无解 |
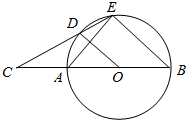 如图,AB是⊙O的直径,延长BA至C,使BC=3AC,过点C作⊙O的割线交⊙O于D、E两点,且∠ADC=∠AOD.
如图,AB是⊙O的直径,延长BA至C,使BC=3AC,过点C作⊙O的割线交⊙O于D、E两点,且∠ADC=∠AOD.