题目内容
19. 正方形ABCD与正方形ABEF互相垂直,点M,N,G分别是AE,BC,CE的中点,AB=2,
正方形ABCD与正方形ABEF互相垂直,点M,N,G分别是AE,BC,CE的中点,AB=2,(1)求证:BE⊥MG
(2)求证:MN∥平面EFDC
(3)求多面体A-EFDC的体积.
分析 (1)由平面ABCD⊥平面ABEF,可得BE⊥AB,进一步得到BE⊥AC,再由中位线定理得到MG∥AC,则BE⊥MG;
(2)由M,N分别为BF,BC的中点,结合中位线定理得MN∥CF,再由线面平行的判断得答案;
(3)由题意可得平面EFDC⊥平面AFD,过A作AH⊥DF交DF于H,可得AH⊥平面EFDC,解直角三角形求得AH=$\sqrt{2}$,代入三棱锥的体积公式求得多面体A-EFDC的体积.
解答 (1)证明:如图,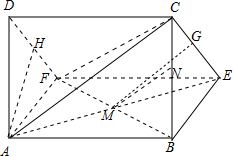
∵平面ABCD⊥平面ABEF,BE⊥AB,∴BE⊥平面ABCD,则BE⊥AC,
由M,G分别为AE,CE的中点,可得MG∥AC,∴BE⊥MG;
(2)证明:连接BF,则M,N分别为BF,BC的中点,∴MN∥CF,
而CF?平面EFDC,MN?平面EFDC,∴MN∥平面EFDC;
(3)解:由题意可得,平面EFDC⊥平面AFD,
又AD=AF,且∠DAF=90°,过A作AH⊥DF交DF于H,
∴AH⊥平面EFDC,在Rt△DAF中,由AD=AF=2,可得AH=$\sqrt{2}$,
∴${V}_{A-EFDC}=\frac{1}{3}×2×2×\sqrt{2}=\frac{4}{3}\sqrt{2}$.
点评 本小题主要考查空间线面关系、几何体的体积等知识,考查数形结合、化归与转化的数学思想方法,以及空间想象能力、推理论证能力和运算求解能力,是中档题.

练习册系列答案
 三新快车金牌周周练系列答案
三新快车金牌周周练系列答案
相关题目
9.椭圆ax2+by2=1与直线y=1-x交于A、B两点,过原点与线段AB中点的直线的斜率为$\frac{\sqrt{3}}{2}$,则$\frac{b}{a}$值为( )
| A. | $\frac{\sqrt{3}}{2}$ | B. | $\frac{2\sqrt{3}}{3}$ | C. | $\frac{9\sqrt{3}}{2}$ | D. | $\frac{2\sqrt{3}}{27}$ |
10.吉安市某工厂车间加工零件的个数x与所花费的时间y之间的线性回归方程为y=0.01x-0.5,则加工600个零件大约需要时间为( )h.
| A. | 0.5 | B. | 3.5 | C. | 5.5 | D. | 6.5 |
7.已知F1、F2为椭圆的两个焦点,以线段F1F2为一边的正方形ABF2F1与椭圆交于M,N两点,且M,N分别为边AF1,BF2的中点,则椭圆的离心率为( )
| A. | $\sqrt{3}$-1 | B. | $\sqrt{5}$-1 | C. | $\frac{\sqrt{3}-1}{2}$ | D. | $\frac{\sqrt{5}-1}{2}$ |
4.已知双曲线的左、右焦点分别为F1,F2,在左支上过F1的弦AB的长为10,若2a=16,则△ABF2的周长是( )
| A. | 32 | B. | 36 | C. | 42 | D. | 52 |
11.下列向量中,可以作为基底的是( )
| A. | $\overrightarrow{{e}_{1}}$=(0,0),$\overrightarrow{{e}_{2}}$=(1,-2) | B. | $\overrightarrow{{e}_{1}}$=(2,-3),$\overrightarrow{{e}_{2}}$=(-$\frac{1}{2}$,$\frac{3}{4}$) | ||
| C. | $\overrightarrow{{e}_{1}}$=(3,5),$\overrightarrow{{e}_{2}}$=(6,10) | D. | $\overrightarrow{{e}_{1}}$=(1,-2),$\overrightarrow{{e}_{2}}$=(5,7) |
8.口袋里装有大小相同的3个白球和2个黑球,每次从中不放回随机抽取1个球,连续抽出2次,则在第一次抽到白球的条件下,第二次抽到白球的概率为( )
| A. | $\frac{3}{5}$ | B. | $\frac{3}{10}$ | C. | $\frac{1}{4}$ | D. | $\frac{1}{2}$ |