题目内容
14．已知点A（-$\sqrt{3}$，1），点B在y轴上，直线AB的倾斜角为120°，则点B的坐标为（0，-2）．分析 由题意设出B的坐标，由两点求出AB所在直线的斜率，结合直线的斜率等于倾斜角的正切值求解．
解答 解：由题意设B（0，m），
又点A（-$\sqrt{3}$，1），直线AB的倾斜角为120°，
∴$k=tan120°=-\sqrt{3}=\frac{m-1}{\sqrt{3}}$，即m=-2．
∴点B的坐标为（0，-2）．
故答案为：（0，-2）．
点评 本题考查直线的倾斜角与斜率，考查了由两点的坐标求直线的斜率，是基础题．
练习册系列答案
相关题目
2．某几何体的三视图如图所示，按图中所给的尺寸，该几何体的体积为（ ）
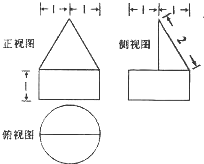
| A． | $\frac{\sqrt{3}π}{6}$+1 | B． | $\frac{\sqrt{3}π}{6}$+π | C． | $\frac{\sqrt{3}π}{3}$+π | D． | $\frac{\sqrt{3}π}{3}$+1 |
正方形ABCD与正方形ABEF互相垂直，点M，N，G分别是AE，BC，CE的中点，AB=2，
6．定义在（0，+∞）的函数f（x）为单调函数，对任意的x∈（0，+∞）恒有f[f（x）-log4x]=5．x0是方程f（x）-f′（x）=4的一个根，则x0所在区间为（ ）
| A． | （1，2） | B． | （2，3） | C． | （3，4） | D． | （4，5） |
3．在空间中，设直线l的方向向量为$\overrightarrow{a}$，平面α的法向量为$\overrightarrow{b}$，对于原命题“若$\overrightarrow{a}$•$\overrightarrow{b}$=0，则l∥α”，下列判断正确的是（ ）
| A． | 原命题为真，否命题为真 | B． | 原命题为假，否命题为假 | ||
| C． | 原命题为假，否命题为真 | D． | 原命题为真，否命题为假 |
4．抛物线x2=4y的焦点到准线的距离为（ ）
| A． | $\frac{1}{2}$ | B． | 1 | C． | 2 | D． | 4 |