题目内容
11.下列向量中,可以作为基底的是( )| A. | $\overrightarrow{{e}_{1}}$=(0,0),$\overrightarrow{{e}_{2}}$=(1,-2) | B. | $\overrightarrow{{e}_{1}}$=(2,-3),$\overrightarrow{{e}_{2}}$=(-$\frac{1}{2}$,$\frac{3}{4}$) | ||
| C. | $\overrightarrow{{e}_{1}}$=(3,5),$\overrightarrow{{e}_{2}}$=(6,10) | D. | $\overrightarrow{{e}_{1}}$=(1,-2),$\overrightarrow{{e}_{2}}$=(5,7) |
分析 平面内任意两个不共线的向量都可以作为基底,判断各个徐昂项中的两个向量是否共线,从而得出结论.
解答 解:平面内任意两个不共线的向量都可以作为基底,由于向量(1,2)和向量(5,7)不共线,
故可以作为基底,
而其它选项中的2个向量的坐标对应成比例,故其它选项中的2个向量是共线向量,不能作为基底,
故选:D.
点评 题主要考查基地的定义,两个向量是否共线的判定方法,属于基础题.

练习册系列答案
相关题目
1.已知定义在R上的函数f(x)满足f(1)=1,且对于任意的x,f′(x)$<\frac{1}{2}$恒成立,则不等式f(lg2x)<$\frac{l{g}^{2}x}{2}$+$\frac{1}{2}$的解集为( )
| A. | (0,$\frac{1}{10}$) | B. | (10,+∞) | C. | ($\frac{1}{10}$,10) | D. | (0,$\frac{1}{10}$)∪(10,+∞) |
2.某几何体的三视图如图所示,按图中所给的尺寸,该几何体的体积为( )
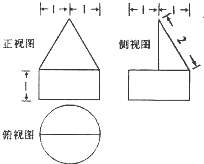

| A. | $\frac{\sqrt{3}π}{6}$+1 | B. | $\frac{\sqrt{3}π}{6}$+π | C. | $\frac{\sqrt{3}π}{3}$+π | D. | $\frac{\sqrt{3}π}{3}$+1 |
6.定义在(0,+∞)的函数f(x)为单调函数,对任意的x∈(0,+∞)恒有f[f(x)-log4x]=5.x0是方程f(x)-f′(x)=4的一个根,则x0所在区间为( )
| A. | (1,2) | B. | (2,3) | C. | (3,4) | D. | (4,5) |
3.在空间中,设直线l的方向向量为$\overrightarrow{a}$,平面α的法向量为$\overrightarrow{b}$,对于原命题“若$\overrightarrow{a}$•$\overrightarrow{b}$=0,则l∥α”,下列判断正确的是( )
| A. | 原命题为真,否命题为真 | B. | 原命题为假,否命题为假 | ||
| C. | 原命题为假,否命题为真 | D. | 原命题为真,否命题为假 |
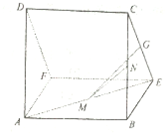 正方形ABCD与正方形ABEF互相垂直,点M,N,G分别是AE,BC,CE的中点,AB=2,
正方形ABCD与正方形ABEF互相垂直,点M,N,G分别是AE,BC,CE的中点,AB=2,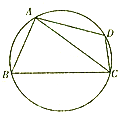 某棚户区改造工程规划用地近似为图中半径为R的圆面,图中圆内接四边形ABCD为拟定拆迁的棚户区,测得AB=AD=4百米,BC=6百米,CD=2百米.
某棚户区改造工程规划用地近似为图中半径为R的圆面,图中圆内接四边形ABCD为拟定拆迁的棚户区,测得AB=AD=4百米,BC=6百米,CD=2百米.