题目内容
(本小题满分14分)
设椭圆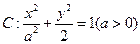 的左右焦点分别为
的左右焦点分别为 、
、 ,
,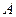 是椭圆
是椭圆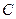 上的一点,
上的一点,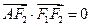 ,坐标原点
,坐标原点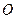 到直线
到直线 的距离为
的距离为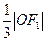 .
.
(1)求椭圆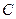 的方程;
的方程;
(2)设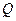 是椭圆
是椭圆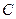 上的一点,过点
上的一点,过点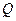 的直线
的直线 交
交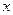 轴于点
轴于点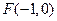 ,交
,交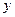 轴于点
轴于点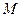 ,若
,若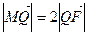 ,求直线
,求直线 的斜率.
的斜率.
设椭圆
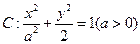 的左右焦点分别为
的左右焦点分别为 、
、 ,
,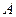 是椭圆
是椭圆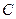 上的一点,
上的一点,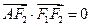 ,坐标原点
,坐标原点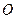 到直线
到直线 的距离为
的距离为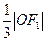 .
.(1)求椭圆
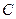 的方程;
的方程;(2)设
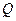 是椭圆
是椭圆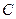 上的一点,过点
上的一点,过点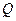 的直线
的直线 交
交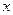 轴于点
轴于点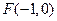 ,交
,交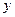 轴于点
轴于点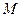 ,若
,若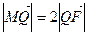 ,求直线
,求直线 的斜率.
的斜率.解:(1)由题设知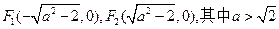
由于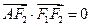 ,则有
,则有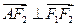 ,所以点
,所以点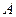 的坐标为
的坐标为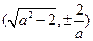 …2分
…2分
故 所在直线方程为
所在直线方程为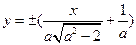
所以坐标原点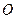 到直线
到直线 的距离为
的距离为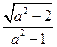 …………………4分
…………………4分
又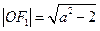 ,所以
,所以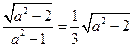 解得:
解得: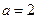
所求椭圆的方程为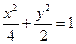 …………………6分
…………………6分
(2)由题意可知直线 的斜率存在,设直线斜率为
的斜率存在,设直线斜率为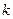 ………………
……………… …7分
…7分
直线 的方程为
的方程为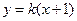 ,则有
,则有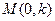
设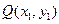 ,由于
,由于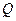 、
、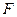 、
、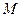 三点共线,且
三点共线,且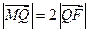
根据题意得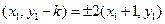 ,解得
,解得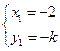 或
或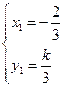 ………10分
………10分
又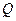 在椭圆
在椭圆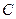 上,故
上,故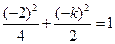 或
或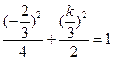 …………………12分
…………………12分
解得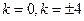 ,综上,直线
,综上,直线 的斜率为
的斜率为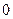 或
或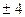 …………………14分
…………………14分
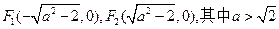
由于
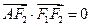 ,则有
,则有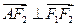 ,所以点
,所以点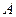 的坐标为
的坐标为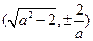 …2分
…2分故
 所在直线方程为
所在直线方程为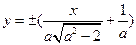
所以坐标原点
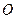 到直线
到直线 的距离为
的距离为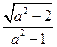 …………………4分
…………………4分又
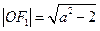 ,所以
,所以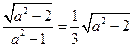 解得:
解得: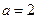
所求椭圆的方程为
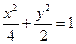 …………………6分
…………………6分(2)由题意可知直线
 的斜率存在,设直线斜率为
的斜率存在,设直线斜率为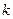 ………………
……………… …7分
…7分直线
 的方程为
的方程为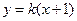 ,则有
,则有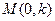
设
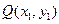 ,由于
,由于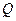 、
、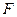 、
、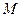 三点共线,且
三点共线,且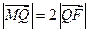
根据题意得
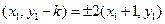 ,解得
,解得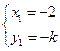 或
或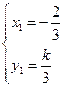 ………10分
………10分又
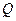 在椭圆
在椭圆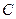 上,故
上,故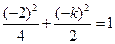 或
或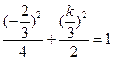 …………………12分
…………………12分解得
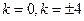 ,综上,直线
,综上,直线 的斜率为
的斜率为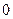 或
或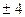 …………………14分
…………………14分略

练习册系列答案
相关题目
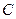 :
: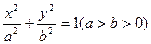 ,
,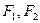 分别为左,右焦点,离心率为
分别为左,右焦点,离心率为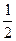 ,点
,点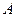 在椭圆
在椭圆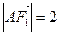 ,
,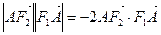 ,过
,过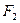 与坐标轴不垂直的直线
与坐标轴不垂直的直线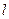 交椭圆于
交椭圆于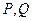 两点.
两点.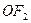 上是否存在点
上是否存在点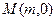 ,使得以线段
,使得以线段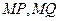 为邻边的四边形是菱形?若存在,求出实数
为邻边的四边形是菱形?若存在,求出实数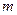 的取值范围;若不存在,说明理由.
的取值范围;若不存在,说明理由. 中,点P到两点
中,点P到两点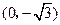 ,
,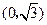 的距离之和等于4,设点P的轨迹为
的距离之和等于4,设点P的轨迹为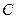 .求出
.求出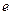 的大小;
的大小;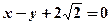 的距离为3.求椭圆的方程
的距离为3.求椭圆的方程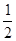 ,焦点是
,焦点是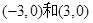 ,则椭圆方程为 ( ■ )
,则椭圆方程为 ( ■ )


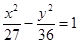
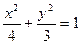 的长轴两端点为
的长轴两端点为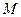 、
、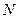 ,异于
,异于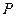 在椭圆上,则
在椭圆上,则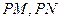 的斜率之积为 .
的斜率之积为 . 的左右焦点为F1,F2,点P在椭圆上,且|PF1|=6,则
的左右焦点为F1,F2,点P在椭圆上,且|PF1|=6,则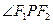 =
=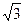 ,-2),Q(-2
,-2),Q(-2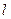 与椭圆
与椭圆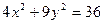 相交于
相交于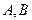 两点,弦
两点,弦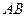 的中点坐标为
的中点坐标为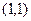 ,则直线
,则直线