题目内容
(本小题满分12分)
已知椭圆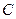 :
: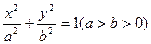 ,
,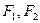 分别为左,右焦点,离心率为
分别为左,右焦点,离心率为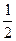 ,点
,点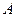 在椭圆
在椭圆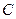 上,
上,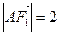 ,
,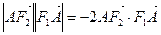 ,过
,过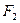 与坐标轴不垂直的直线
与坐标轴不垂直的直线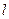 交椭圆于
交椭圆于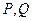 两点.
两点.
(Ⅰ)求椭圆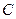 的方程;
的方程;
(Ⅱ)在线段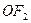 上是否存在点
上是否存在点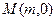 ,使得以线段
,使得以线段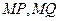 为邻边的四边形是菱形?若存在,求出实数
为邻边的四边形是菱形?若存在,求出实数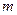 的取值范围;若不存在,说明理由.
的取值范围;若不存在,说明理由.
已知椭圆
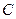 :
: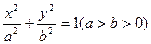 ,
,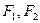 分别为左,右焦点,离心率为
分别为左,右焦点,离心率为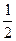 ,点
,点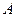 在椭圆
在椭圆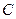 上,
上,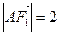 ,
,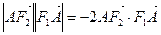 ,过
,过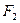 与坐标轴不垂直的直线
与坐标轴不垂直的直线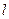 交椭圆于
交椭圆于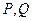 两点.
两点.(Ⅰ)求椭圆
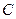 的方程;
的方程;(Ⅱ)在线段
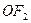 上是否存在点
上是否存在点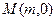 ,使得以线段
,使得以线段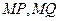 为邻边的四边形是菱形?若存在,求出实数
为邻边的四边形是菱形?若存在,求出实数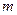 的取值范围;若不存在,说明理由.
的取值范围;若不存在,说明理由.解:(1)由已知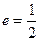 ,所以
,所以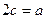 ,
,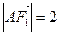 ,
,
又因为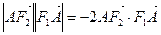 ,所以
,所以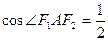 ,--------------------------------2分
,--------------------------------2分
由余弦定理 ,----4分
,----4分
所以 ,
, ,所以椭圆方程为
,所以椭圆方程为 .-------------------------------5分
.-------------------------------5分
(2)假设存在点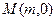 满足条件,设
满足条件,设 ,
, ,直线
,直线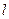 的方程为
的方程为 ,
,
联立: ,则
,则
 ,----------------------------------------------------------------------------7分
,----------------------------------------------------------------------------7分

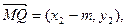
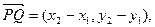

由题知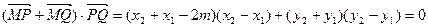 ,
,
因为 ,
,
所以 ,即
,即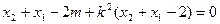 ,
,
则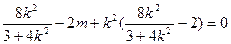 ,
,
所以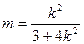 ,---------------------------------------------------------------------10分
,---------------------------------------------------------------------10分
 ,又
,又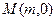 在线段
在线段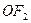 上,则
上,则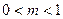 ,
,
故存在 满足题意.-----------------12分
满足题意.-----------------12分
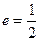 ,所以
,所以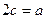 ,
,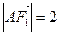 ,
,
又因为
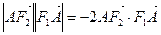 ,所以
,所以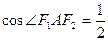 ,--------------------------------2分
,--------------------------------2分由余弦定理
 ,----4分
,----4分所以
 ,
, ,所以椭圆方程为
,所以椭圆方程为 .-------------------------------5分
.-------------------------------5分(2)假设存在点
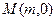 满足条件,设
满足条件,设 ,
, ,直线
,直线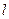 的方程为
的方程为 ,
,联立:
 ,则
,则 ,----------------------------------------------------------------------------7分
,----------------------------------------------------------------------------7分
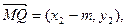
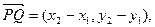

由题知
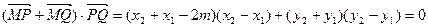 ,
,因为
 ,
,所以
 ,即
,即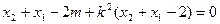 ,
,则
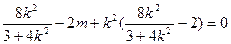 ,
,
所以
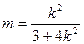 ,---------------------------------------------------------------------10分
,---------------------------------------------------------------------10分 ,又
,又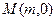 在线段
在线段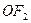 上,则
上,则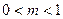 ,
,故存在
 满足题意.-----------------12分
满足题意.-----------------12分略

练习册系列答案
相关题目
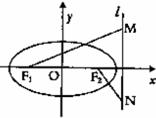
 的左右焦点为
的左右焦点为 ,抛物线C:
,抛物线C: 以F2为焦点且与椭圆相交于点M
以F2为焦点且与椭圆相交于点M 、N
、N ,直线
,直线 与抛物线C相切
与抛物线C相切
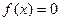 的解;
的解;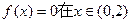 上有两个解
上有两个解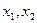 ,求k取值范围并证明
,求k取值范围并证明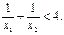
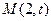
 在直线
在直线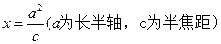 上。
上。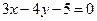 截得的弦长为2的圆的方程;
截得的弦长为2的圆的方程;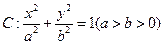 的离心率为
的离心率为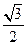 ,短轴的一个端点到右焦点的距离为
,短轴的一个端点到右焦点的距离为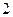 .设直线
.设直线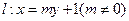 与椭圆
与椭圆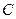 相交于
相交于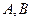 两点,点
两点,点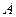 关于
关于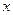 轴对称点为
轴对称点为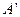 .
.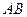 为直径的圆过坐标原点
为直径的圆过坐标原点
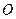 ,求直线
,求直线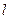 的方程;
的方程; 变化时,直线
变化时,直线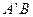 与
与
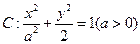 的左右焦点分别为
的左右焦点分别为 、
、 ,
,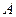 是椭圆
是椭圆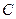 上的一点,
上的一点,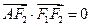 ,坐标原点
,坐标原点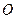 到直线
到直线 的距离为
的距离为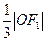 .
.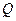 是椭圆
是椭圆 交
交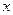 轴于点
轴于点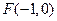 ,交
,交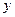 轴于点
轴于点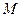 ,若
,若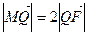 ,求直线
,求直线 ,双曲线
,双曲线 ,抛物线
,抛物线 (其中
(其中 的离心率分别为
的离心率分别为 ,则
,则
 的值为 ( )
的值为 ( ) 





 与
与 有关
有关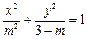 的一个焦点为
的一个焦点为 ,则
,则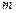 等于 .
等于 .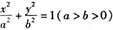 的左、右焦点分别为F1 F2,以F1 F2为直径的圆与椭圆在y轴左侧的部分交于A,B两点,且ΔF2AB是等边三角形,则椭圆的离心率为______
的左、右焦点分别为F1 F2,以F1 F2为直径的圆与椭圆在y轴左侧的部分交于A,B两点,且ΔF2AB是等边三角形,则椭圆的离心率为______