题目内容
一圆形纸片的圆心为原点O,点Q是圆外的一定点,A是圆周上一点,把纸片折叠使点A与点Q重合,然后展开纸片,折痕CD与OA交于P点,当点A运动时P的轨迹是
| A.椭圆 | B.双曲线 | C.抛物线 | D.圆 |
B
专题:计算题;数形结合.
分析:根据CD是线段AQ的垂直平分线.可推断出|PA|=|PQ|,进而可知|PO|-|PQ|=|PO|-|PA|=|OA|结果为定值,进而根据双曲线的定义推断出点P的轨迹.
解答:解:由题意知,CD是线段AQ的垂直平分线.
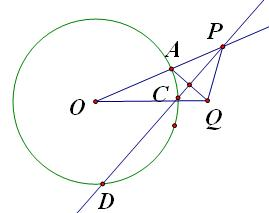
∴|PA|=|PQ|,
∴|PO|-|PQ|=|PO|-|PA|=|OA|(定值),
∴根据双曲线的定义可推断出点P轨迹是以Q、O两点为焦点的双曲线,
故选B.
点评:本题主要考查了双曲线的定义的应用,考查了学生对椭圆基础知识的理解和应用,属于基础题.

练习册系列答案
相关题目
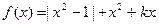
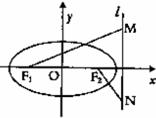
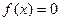 的解;
的解;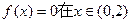 上有两个解
上有两个解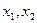 ,求k取值范围并证明
,求k取值范围并证明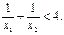
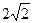 ,0)和F2(
,0)和F2( 交椭圆C于A
交椭圆C于A B两点,且线段AB的中点坐标是P(-
B两点,且线段AB的中点坐标是P(-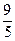 ,
,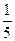 ),求直线
),求直线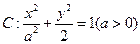 的左右焦点分别为
的左右焦点分别为 、
、 ,
,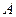 是椭圆
是椭圆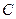 上的一点,
上的一点,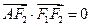 ,坐标原点
,坐标原点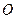 到直线
到直线 的距离为
的距离为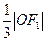 .
.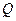 是椭圆
是椭圆 交
交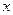 轴于点
轴于点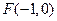 ,交
,交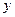 轴于点
轴于点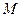 ,若
,若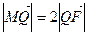 ,求直线
,求直线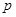 是椭圆
是椭圆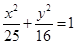 上的点.若
上的点.若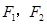 是椭圆的两个焦点,则
是椭圆的两个焦点,则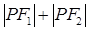 等于( )
等于( )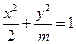 的离心率为
的离心率为 ,则
,则 = .
= .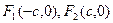 为椭圆
为椭圆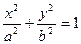 的两个焦点,P为椭圆上一点且
的两个焦点,P为椭圆上一点且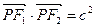 ,则此椭圆离心率的取值范围是 ( ▲ )
,则此椭圆离心率的取值范围是 ( ▲ )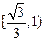
 的两个焦点为
的两个焦点为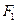 、
、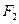 ,点
,点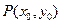 满足
满足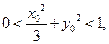 则
则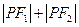 的取值范围为 ,直线
的取值范围为 ,直线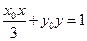 与椭圆
与椭圆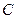 的公共点的个数为
的公共点的个数为 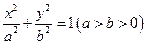 的两个焦点为
的两个焦点为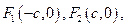
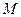 是椭圆上一点,且满
是椭圆上一点,且满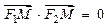 .
.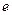 的取值
的取值 范围;
范围;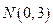 到椭圆上点的最远距离为
到椭圆上点的最远距离为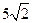 .
.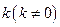 的直线
的直线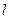 与椭圆G相交于不同两点
与椭圆G相交于不同两点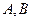 ,
,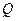 为
为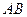 的中点,问:
的中点,问: