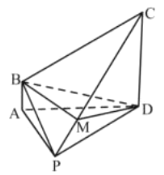
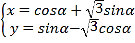题目内容
【题目】抛物线上任意两点![]()
![]() 处的切线交于点
处的切线交于点![]() ,称
,称![]() 为“阿基米德三角形”.当线段
为“阿基米德三角形”.当线段![]() 经过抛物线焦点
经过抛物线焦点![]() 时,
时,![]() 具有以下特征:①
具有以下特征:①![]() 点必在抛物线的准线上;②
点必在抛物线的准线上;②![]() 为直角三角形,且
为直角三角形,且![]() ;③
;③![]() .若经过抛物线
.若经过抛物线![]() 焦点的一条弦为
焦点的一条弦为![]() ,阿基米德三角形为
,阿基米德三角形为![]() ,且点
,且点![]() 的纵坐标为4,则直线
的纵坐标为4,则直线![]() 的方程为( )
的方程为( )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
【答案】A
【解析】
由△PAB为“阿基米德三角形”,且线段AB经过抛物线![]() 焦点,可得:P点必在抛物线的准线上,可求出点P(1,4),从而得到直线PF的斜率为2,又
焦点,可得:P点必在抛物线的准线上,可求出点P(1,4),从而得到直线PF的斜率为2,又![]() ,所以直线AB的斜率为
,所以直线AB的斜率为![]() ,再利用点斜式即可求出直线AB的方程.
,再利用点斜式即可求出直线AB的方程.
解:由题意可知,抛物线y2=4x的焦点F的坐标为(1,0),准线方程为:x=﹣1,由△PAB为“阿基米德三角形”,且线段AB经过抛物线y2=4x焦点,可得:P点必在抛物线的准线上,
∴点P(﹣1,4),
∴直线PF的斜率为:![]() =﹣2,
=﹣2,
又∵PF⊥AB,
∴直线AB的斜率为![]() ,
,
∴直线AB的方程为:y﹣0=![]() ,即x﹣2y﹣1=0,
,即x﹣2y﹣1=0,
故选:A.

练习册系列答案
 步步高口算题卡系列答案
步步高口算题卡系列答案 点睛新教材全能解读系列答案
点睛新教材全能解读系列答案 小学教材完全解读系列答案
小学教材完全解读系列答案
相关题目