题目内容
【题目】在直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为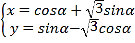 (
(![]() 为参数),以坐标原点
为参数),以坐标原点![]() 为极点,
为极点,![]() 轴的正半轴为极轴,取相同长度单位建立极坐标系,直线
轴的正半轴为极轴,取相同长度单位建立极坐标系,直线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(Ⅰ)求曲线![]() 和直线
和直线![]() 的直角坐标方程;
的直角坐标方程;
(Ⅱ)直线![]() 与
与![]() 轴交点为
轴交点为![]() ,经过点
,经过点![]() 的直线与曲线
的直线与曲线![]() 交于
交于![]() ,
,![]() 两点,证明:
两点,证明:![]() 为定值.
为定值.
【答案】(Ⅰ)曲线![]() :
:![]() .
.![]() 的直角坐标方程为
的直角坐标方程为![]() .(Ⅱ)见证明
.(Ⅱ)见证明
【解析】
(Ⅰ)根据曲线的参数方程,平方相加,即可求得曲线![]() 普通方程,再根据极坐标方程与直角坐标方程的互化公式,即可得到直线的直角坐标方程.
普通方程,再根据极坐标方程与直角坐标方程的互化公式,即可得到直线的直角坐标方程.
(Ⅱ)设过点![]() 的直线方程为
的直线方程为![]() (
(![]() 为参数),代入曲线的普通方程,根据参数的几何意义,即可求解.
为参数),代入曲线的普通方程,根据参数的几何意义,即可求解.
(Ⅰ)由题意,可得![]() ,
,
化简得曲线![]() :
:![]() .
.
直线![]() 的极坐标方程展开为
的极坐标方程展开为![]() ,
,
故![]() 的直角坐标方程为
的直角坐标方程为![]() .
.
(Ⅱ)显然![]() 的坐标为
的坐标为![]() ,不妨设过点
,不妨设过点![]() 的直线方程为
的直线方程为![]() (
(![]() 为参数),
为参数),
代入![]() :
:![]() 得
得![]() ,
,
所以![]() 为定值.
为定值.

练习册系列答案
相关题目