题目内容
【题目】已知函数f(x)=|x-m|-|2x+2m|(m>0).
(Ⅰ)当m=1时,求不等式f(x)≥1的解集;
(Ⅱ)若x∈R,t∈R,使得f(x)+|t-1|<|t+1|,求实数m的取值范围.
【答案】(Ⅰ)[-2,-![]() ];(Ⅱ)0<m<1
];(Ⅱ)0<m<1
【解析】
(Ⅰ)分段去绝对值解不等数组后在相并可得;
(Ⅱ)f(x)+|t-1|<|t+1|f(x)<|t+1|-|t-1|对任意x∈R恒成立,对实数t有解.
再利用分段函数的单调性求得f(x)的最大值,根据绝对值不等式的性质可得|t+1|-|t-1|的最大值,然后将问题转化为f(x)的最大值<(|t+1|-|t-1|)的最大值可得.
(Ⅰ)当m=1时,|x-1|-|2x+2|≥1![]() 或
或![]() 或
或![]() ,
,
解得-2≤x≤-![]() ,所以原不等式的解集为[-2,-
,所以原不等式的解集为[-2,-![]() ].
].
(Ⅱ)f(x)+|t-1|<|t+1|f(x)<|t+1|-|t-1|对任意x∈R恒成立,对实数t有解.
∵f(x)=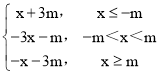 ,
,
根据分段函数的单调性可知:x=-m时,f(x)取得最大值f(-m)=2m,
∵||t+1|-|t-1||≤|(t+1)-(t-1)|=2,
∴-2≤|t+1|-|t-1|≤2,即|t+1|-|t-1|的最大值为2.
所以问题转化为2m<2,解得0<m<1.

【题目】某校为了解学生对消防安全知识的掌握情况,开展了网上消防安全知识有奖竞赛活动,并对参加活动的男生、女生各随机抽取20人,统计答题成绩,分别制成如下频率分布直方图和茎叶图:
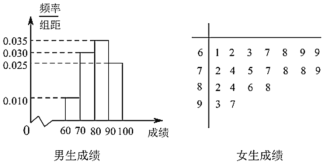
(1)把成绩在80分以上(含80分)的同学称为“安全通”.根据以上数据,完成以下![]() 列联表,并判断是否有95%的把握认为是否是“安全通”与性别有关
列联表,并判断是否有95%的把握认为是否是“安全通”与性别有关
男生 | 女生 | 合计 | |
安全通 | |||
非安全通 | |||
合计 |
(2)以样本的频率估计总体的概率,现从该校随机抽取2男2女,设其中“安全通”的人数为![]() ,求
,求![]() 的分布列与数学期望.
的分布列与数学期望.
附:参考公式![]() ,其中
,其中![]() .
.
参考数据:
| 0.100 | 0.050 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
【题目】某公司培训员工某项技能,培训有如下两种方式:
方式一:周一到周五每天培训1小时,周日测试
方式二:周六一天培训4小时,周日测试
公司有多个班组,每个班组60人,现任选两组![]() 记为甲组、乙组
记为甲组、乙组![]() 先培训;甲组选方式一,乙组选方式二,并记录每周培训后测试达标的人数如表:
先培训;甲组选方式一,乙组选方式二,并记录每周培训后测试达标的人数如表:
第一周 | 第二周 | 第三周 | 第四周 | |
甲组 | 20 | 25 | 10 | 5 |
乙组 | 8 | 16 | 20 | 16 |
![]() 用方式一与方式二进行培训,分别估计员工受训的平均时间
用方式一与方式二进行培训,分别估计员工受训的平均时间![]() 精确到
精确到![]() ,并据此判断哪种培训方式效率更高?
,并据此判断哪种培训方式效率更高?
![]() 在甲乙两组中,从第三周培训后达标的员工中采用分层抽样的方法抽取6人,再从这6人中随机抽取2人,求这2人中至少有1人来自甲组的概率.
在甲乙两组中,从第三周培训后达标的员工中采用分层抽样的方法抽取6人,再从这6人中随机抽取2人,求这2人中至少有1人来自甲组的概率.
【题目】最近,纪录片《美国工厂》引起中美观众热议,大家都认识到,大力发展制造业,是国家强盛的基础,而产业工人的年龄老化成为阻碍美国制造业发展的障碍,中国应未雨绸缪.某工厂有35周岁以上(含35周岁)工人300名,35周岁以下工人200名,为研究工人的日平均生产量是否与年龄有关.现采用分层抽样的方法,从中抽取了100名工人,先统计了他们某月的日平均生产件数,然后按工人年龄在“35周岁以上(含35周岁)”和“35周岁以下”分为两组,在将两组工人的日平均生产件数分成5组:![]() 分别加以统计,得到如图所示的频率分布直方图.
分别加以统计,得到如图所示的频率分布直方图.
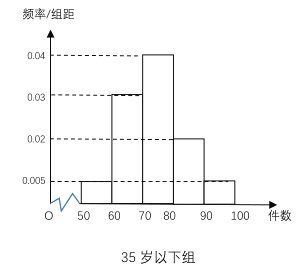
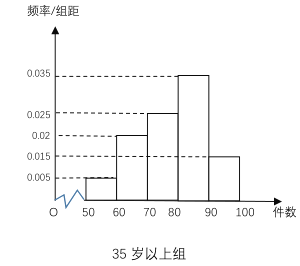
(1)从样本中日平均生产件数不足60件的工人中随机抽取2人,求至少抽到一名“35周岁以下组”工人的概率.
(2)规定日平均生产件数不少于80件者为“生产能手”,请你根据已知条件完成![]() 的列联表,并判断是否有95%的把握认为“生产能手与工人所在的年龄组有关”?
的列联表,并判断是否有95%的把握认为“生产能手与工人所在的年龄组有关”?
生产能手 | 非生产能手 | 合计 | |
35岁以下 | |||
35岁以上 | |||
合计 |
附表: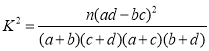
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |