Question

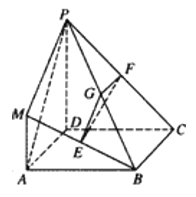
【题目】如图（1）是一直角墙角，，墙角的两堵墙面和地面两两互相垂直.是一块长为米，宽为米的板材，现欲用板材与墙角围成一个直棱柱空间堆放谷物.

（1）若按如图（1）放置，如何放置板材才能使这个直棱柱空间最大？

（2）由于墙面使用受限，面只能使用米，面只能使用米.此矩形板材可以折叠围成一个直四棱柱空间，如图（2），如何折叠板材才能使这个空间最大？

Answer 1

【答案】(1) 板材与墙面成45°角;(2)见解析.

【解析】分析：（1）设，且 因为直三棱柱的高为定值，故底面面积最大时体积最大，利用基本不等式可得；（2）因为直四棱柱的高为定值，故底面面积最大时体积最大，又的面积为定值，只需寻找面积的最大值，作只需最大即可，设则，可得，利用二次函数的性质可得结果.

详解：（1）设，且

因为直三棱柱的高为定值，故底面面积最大时体积最大

，

当且仅当取到等号.

即板材放置时，使得板材与墙面成45°角.

（2）因为直四棱柱的高为定值，故底面面积最大时体积最大，又的面积为定值，只需寻找面积的最大值.

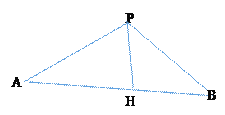又在中，只需寻找AB边上高的最大值即可.

如图：作

设则

当时PH最大,此时

即板材放置时，沿中间折叠，使得PA=PB.