题目内容
【题目】在如图所示的几何体中，四边形
是正方形， 
平面， 
分别为
的中点，且
.
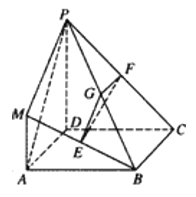
（1）求证：平面
平面
；
（2）求证：平面P
；
【答案】（1）证明过程详见解析（2）证明过程详见解析；
【解析】
(1)由三角形中位线定理可得
，由正方形的性质可得
，
，由线面平行的判定定理可得
平面
， 
平面，从而可得结果；(2)由线面垂直的性质证明
,正方形的性质可得
，结合
，可得
平面
，从而可得平面
平面 ；
(1)∵
分别为
的中点，
∴，
又∵四边形
是正方形，
∴，∴，
∵
在平面外， 
在平面内，
∴平面， 平面，
又∵都在平面
内且相交，
∴平面
平面.
(2)证明：由已知
平面
，
∴
平面.
又
平面，∴.
∵四边形为正方形，∴，
又
，∴
平面，
在
中，∵
分别为
的中点，
∴，∴平面.
又
平面，∴平面平面.
练习册系列答案
相关题目
【题目】某商店为了解气温对某产品销售量的影响，随机记录了该商店
月份中
天的日销售量
（单位：千克）与该地当日最低气温
（单位：℃）的数据，如表所示：
|
|
|
|
|
|
|
|
|
|
|
|
（1）求与的回归方程
：
（2）判断与之间是正相关还是负相关；若该地月份某天的最低气温为
，请用（1）中的回归方程预测该商店当日的销售量．
参考公式：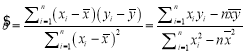
，
．
